Thermocapillary instability in full-zone liquid bridges

Description: This work has addressed some aspects of the stability of steady axisymmetric melt flows occurring in cylindrical floating-zone configurations, and is the continuation of a project first described in the WIAS 2001 yearly report ([1]). The initial aim of the project was to investigate flow and thermal effects nonlinearly for low Prandtl number (Pr) within a sub-critical framework. In [2] full numerical results from direct simulation (based on solving the unsteady incompressible axisymmetric Navier-Stokes and heat-transport equations) were presented for a wide range of domain aspect ratios; it was found that for both sufficiently ``wide'' domains (that is, having a radius-to-height ratio r_c exceeding 2, roughly) and ``narrow'' domains (r_c < 0.3, approx.) the results showed very good agreement with corresponding results obtained from (asymptotically) reduced models in each case.

Moreover, the (slender-flow) approximation for narrow domains provided considerable insight into the structure of the flow solution, especially in the case of Marangoni convection under zero buoyancy; as the thermo-capillary stress (proportional to the dynamic Reynolds number, Re_D) is increased at the liquid/gas interface, a strong jet-like flow regime is found to emerge around the mid-zone, where the two counter-rotating, axially-aligned tori (which characterize the basic flow) merge.

**Fig. 1:** Sub-critical mid-zone-analysis result from a slender-flow model depicting scaled local pressure gradient (q) versus scaled dynamic Reynolds number (AM), in the left-hand plot; radial profiles of radial ( $\tilde{u}$ ) and axial ( $\tilde{w}$ ) velocity components at the mid-height on the upper (`+') and lower (`-') branches, for AM = 2.43, in the right-hand plot; see [2] for further details.
$\makeatletter \@ZweiProjektbilderNocap[h]{8.29cm}{fig_davis_1b.ps}{fig_davis_2a.ps} \makeatother$

Numerical analysis of the (nonlinear) reduced-model mid-zone equations reveals several important properties: (a) if the system has a solution, then it is not generally unique; (b) the flow cannot remain steady and axisymmetric, beyond a critical value of AM : = r_c³Re_D ( $\approx$ 3.31), the scaled dynamic Reynolds number (see ). However, the (transient) DNS solutions were found to be exclusively ``upper branch'' in type, regardless of the initial conditions used, which would seem to suggest that the ``lower branch'' is a less probable solution form, in practice.

To investigate the possible solution forms beyond the critical Reynolds number, a series of supercritical flows were simulated (with a fixed Prandtl number of 0.02 and zero buoyancy). The following variational system

$\displaystyle {\frac{{d}}{{dt}}}$ $\displaystyle \int\limits_{{\Omega}}^{}$ u^.v d $\displaystyle \Omega$ + $\displaystyle \int\limits_{{\Omega}}^{}$ $\displaystyle \nabla$ u : $\displaystyle \nabla$ v d $\displaystyle \Omega$ - $\displaystyle \int\limits_{{\Omega}}^{}$ p $\displaystyle \nabla$ ^.v d $\displaystyle \Omega$

+ $\displaystyle \int\limits_{{\Omega}}^{}$ [(u^. $\displaystyle \nabla$ )u]^.v d $\displaystyle \Omega$ - $\displaystyle \int\limits_{{\Gamma_{LG}}}^{}$ (u^. $\displaystyle \hat{{\mathbf{e}}}_{{\theta}}^{}$ )(v^. $\displaystyle \hat{{\mathbf{e}}}_{{\theta}}^{}$ ) dS = - Re_Dr_c $\displaystyle \int\limits_{{\Gamma_{LG}}}^{}$ $\displaystyle \nabla$ T_D^.v dS

(1a)

$\displaystyle \int\limits_{{\Omega}}^{}$ ( $\displaystyle \nabla$ ^.u)w d $\displaystyle \Omega$ = 0,

(1b)

$\displaystyle {\frac{{d}}{{dt}}}$ $\displaystyle \int\limits_{{\Omega}}^{}$ TX d $\displaystyle \Omega$ + $\displaystyle {\frac{{1}}{{Pr}}}$ $\displaystyle \int\limits_{{\Omega}}^{}$ $\displaystyle \nabla$ T^. $\displaystyle \nabla$ X d $\displaystyle \Omega$ + $\displaystyle \int\limits_{{\Omega}}^{}$ [(u^. $\displaystyle \nabla$ )T]X d $\displaystyle \Omega$ = 0,

(1c)

which is derived from the governing equations and boundary conditions for the floating-zone configuration ([2]), was solved by a standard finite element method using P₂ - P₁ Taylor-Hood tetrahedra. To discretize in time, a three-step operator-splitting scheme for the momentum part, combined with a Crank-Nicholson scheme for the heat transport equation, was applied. Here $\Omega$ denotes the volume of melt while $\Gamma_{{LG}}^{}$ is the liquid-gas interface; also u is the melt velocity, p the melt pressure, T the melt temperature, T_D the (imposed) temperature on $\Gamma_{{LG}}^{}$ , and t time, whereas v, w, and X are appropriate test functions. Our numerical results have indicated that the melt flow undergoes a transition from a steady axisymmetric state to a non-oscillatory three-dimensional one, for any given aspect ratio of the bridge. This result is wholly consistent with well-established half-zone results ([3], [4]) and suggests that certain characteristics of the instability mechanism are essentially unchanged for the more realistic full-zone model.

**Fig. 2:** Fourier-mode transient behavior for Re_D = 2500 , Pr = 0.02 , r_c = 0.5 indicating the coefficients of axial velocity ( (r, z) = (0.5, 0.25) blue solid line, (0.5, 0.5) red dash line, (0.5, 0.75) green dash-dot line.)
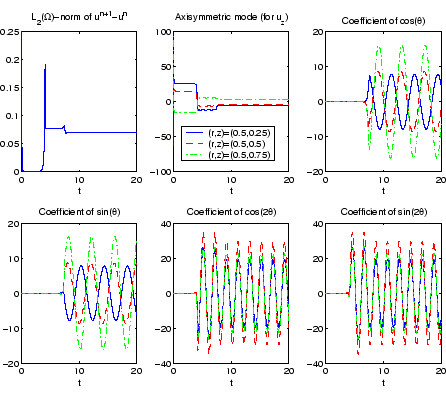$\ProjektEPSbildNocap{0.5\textwidth}{fig2_fz.eps}$

In fig2_dd.eps, computational results are shown for Re_D = 2500, Pr = 0.02, and r_c = 0.5 with T_D $\equiv$ sin( $\pi$ z) and a zero solution as input. The transient behavior of the Fourier (angle) modes for axial velocity at selected points in the domain is mainly portrayed, and from these plots several distinct phases are discernible: (a) the switch to an (unstable) axisymmetric state, at the start; (b) the brief, dominant linear growth of the m = 2 mode; (c) the subsequent weakly-nonlinear interaction of the m = 0 and m = 2 modes, which stabilizes both modes; (d) the later linear growth of the m = 1 mode, leading to a significantly asymmetric state. From numerical linear instability analysis for half zones ([3], [4]), it is known that for aspect ratios lying between 0.3 and 0.68 approximately, the m = 2 mode dominates, which is consistent with the example shown; moreover, in general, the azimuthal number of the most dangerous mode tends to increase with increasing aspect ratio, again in line with half-zone findings.