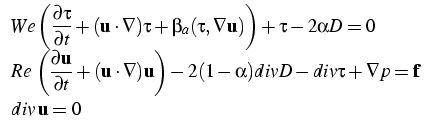
|
|
|
[Contents] | [Index] |
Description: This work is realized in the framework of my dissertation under the supervision of Prof. Dr. E. Bänsch. In nature, there are many fluids that do not satisfy the Newtonian constitutive law. This is also the case of many fluids created for industrial purposes. Fluids like multi-grade oils, liquid detergents, shampoos, dyes, adhesives, biological fluids like blood, paints, greases, printing inks, industrial suspensions, polymer solutions, and polymer melts, fall within the category of non-Newtonian fluids.
The numerical simulation of many industrial problems has been carried
out using viscoelastic models of the Oldroyd kind.
The aim of this work is to develop a mixed
finite element method for the
computation of instationary, incompressible non-Newtonian fluid flow.
Viscoelastic fluid models of Oldroyd type are considered.
The dimensionless constitutive, momentum, and continuity equations,
respectively, for
the Oldroyd fluid model are:
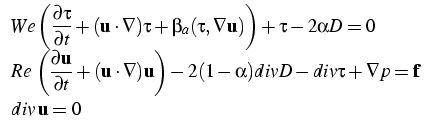
where
![]() (
(![]() ,
,![]()
![]() ) : =
) : = ![]() (
(![]()
![]()
![]() +
+ ![]()
![]()
![]() ) -
) - ![]() (
(![]()
![]()
![]() +
+ ![]()
![]()
![]() ), a
), a ![]() [- 1, 1]
[- 1, 1]
(a = 1 corresponds to the Oldroyd-B model).
The unknown fields are the symmetric stress tensor
![]() :
: ![]() + x
+ x ![]()
![]()
![]() N2s,
the velocity field
u :
N2s,
the velocity field
u : ![]() + x
+ x ![]()
![]()
![]() N,
and the pressure field
p :
N,
and the pressure field
p : ![]() + x
+ x ![]()
![]()
![]() ,
where
,
where
![]()
![]()
![]() N , N = 2, 3.
N , N = 2, 3.
Initial conditions and boundary conditions of Dirichlet type for the velocities and a condition for the stresses on the upstream boundary section have to be added.
Three parameters characterize the flow: the Reynolds number Re ![]() 0,
the fraction of viscoelastic viscosity
0,
the fraction of viscoelastic viscosity
![]()
![]() [0, 1], and
the Weissenberg number We
[0, 1], and
the Weissenberg number We ![]() 0.
This system includes the Navier-Stokes system as a particular case
(
We = 0,
0.
This system includes the Navier-Stokes system as a particular case
(
We = 0,![]() = 0), so it is favorable to develop a numerical method
which can generalize an existing one used for the Navier-Stokes system.
= 0), so it is favorable to develop a numerical method
which can generalize an existing one used for the Navier-Stokes system.
There are two aspects which must be discussed for this system: the finite element spatial discretization and the time discretization.
The solution of Oldroyd's problem by the finite element method presents a difficulty due to the hyperbolic character of the constitutive equation.
This hyperbolic character implies that
some upwinding is needed. The choice of the upwinding technique depends on the
choice of the finite element space used to approximate ![]() .
Since no continuity requirement is needed on
.
Since no continuity requirement is needed on ![]() at interfaces between
elements, as shown in [2], this will be done by
using the discontinuous Galerkin method, which allows the computation of
each component of
at interfaces between
elements, as shown in [2], this will be done by
using the discontinuous Galerkin method, which allows the computation of
each component of ![]() on an element-by-element basis.
For fixed
on an element-by-element basis.
For fixed ![]() the last two
equations are a Stokes system in the variables
the last two
equations are a Stokes system in the variables ![]() and p.
To solve the Stokes system, a mixed finite element method was used:
the stable Taylor-Hood element on unstructured simplicial grids, i.e.
piecewise-quadratic basis functions for the velocity and piecewise-linear
for the pressure.
and p.
To solve the Stokes system, a mixed finite element method was used:
the stable Taylor-Hood element on unstructured simplicial grids, i.e.
piecewise-quadratic basis functions for the velocity and piecewise-linear
for the pressure.
Major numerical problems for the instationary Oldroyd system arise due to
the incompressibility condition, the strong nonlinearity in the momentum
equation, the transport of the stress, the strong coupling of the
unknowns, and stability versus accuracy of the numerical scheme.
The decoupled computation of stress, velocity, and pressure is performed
with an algorithm involving a time approximation based on the
fractional ![]() -scheme ([3]) and on the
splitting method introduced by Saramito
([6]).
As an operator splitting method, the
-scheme ([3]) and on the
splitting method introduced by Saramito
([6]).
As an operator splitting method, the ![]() -scheme
was used, e.g., by Bänsch for the Navier-Stokes equations
([1]).
The method consists of splitting each time interval
[tn, tn+1]
of length
-scheme
was used, e.g., by Bänsch for the Navier-Stokes equations
([1]).
The method consists of splitting each time interval
[tn, tn+1]
of length ![]() t into three subintervals
[tn, tn +
t into three subintervals
[tn, tn + ![]()
![]() t],
[tn +
t],
[tn + ![]()
![]() t, tn + (1 -
t, tn + (1 - ![]() )
)![]() t], and,
[tn + (1 -
t], and,
[tn + (1 - ![]() )
)![]() t, tn+1], and integrating the equations on
each of these subintervals.
t, tn+1], and integrating the equations on
each of these subintervals.
For the Navier-Stokes equations this scheme is second-order accurate,
non-dissipative, and A-stable. Stability and convergence analysis of the
fractional step ![]() -scheme for the unsteady Navier-Stokes equations
are proven in [4] and [5].
Due to the complexity of the splitting method for the Oldroyd system,
only the stability in the linearized case could be proved.
The spectral analysis of the splitting scheme for the linearized
equation system in Fourier space shows very good properties of this scheme
(
-scheme for the unsteady Navier-Stokes equations
are proven in [4] and [5].
Due to the complexity of the splitting method for the Oldroyd system,
only the stability in the linearized case could be proved.
The spectral analysis of the splitting scheme for the linearized
equation system in Fourier space shows very good properties of this scheme
(
![]() = wave vector):
= wave vector):
For the numerical realization of the algorithm, the following subproblems
and solvers are used: in the first and third step,
a Stokes problem (CG), for the second step, a Burgers-like
subproblem (GMRES) and a stress-transport problem
(GMRES discontinuous Galerkin FEM scheme) are to be
solved.
To prove the correctness of the algorithm implementation, the experimental order of converges (EOC) was calculated. The EOC is defined by:
EOCh : = 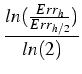 ,
with errors
Errh =
,
with errors
Errh = ![]() | u( . , t)-uh( . , t)|
and grid size h.
| u( . , t)-uh( . , t)|
and grid size h.
The table below contains EOC tests for different norms of the
unknown of the Oldroyd system. The numerical results are presented for
two examples. For each example, computations with Re = 1.0,
![]() = 0.89,
and different values of We are presented.
| . |dg
is the norm used in the discontinuous Galerkin method for error estimation.
= 0.89,
and different values of We are presented.
| . |dg
is the norm used in the discontinuous Galerkin method for error estimation.
| We | | p - ph|L2 | | p - ph|H1 | | u - uh|L2 | | u - uh|H1 |
| |
| |
| 1.0 | 2.2563 | 1.1283 | 2.3071 | 1.3095 | 2.1580 | 1.6599 |
| 4.0 | 2.4671 | 1.1959 | 2.3036 | 1.3586 | 2.1354 | 1.6317 |
| 40.0 | 2.1266 | 1.0343 | 2.5759 | 1.5868 | 2.0295 | 1.4994 |
| 0.5 | 2.0734 | 1.0306 | 2.7892 | 1.7899 | 2.1941 | 1.8746 |
| 1.0 | 2.1578 | 1.078 | 2.9616 | 1.9939 | 2.036 | 1.5056 |
| 10.0 | 2.2528 | 1.1113 | 3.4107 | 2.5078 | 2.0345 | 1.4937 |
The numerical algorithm is implemented in ALBERT,
an adaptive hierarchical finite element toolbox ([7]).
The described method is applied to the computation of the flow in a plane 4:1 contraction, subject to specified boundary conditions. Such a flow is of interest from both a theoretical and a practical point of view (e.g., in relation to polymer processing problems). Experiments show increasing recirculating zones when the Weissenberg number We increases. Similarly growth of the recirculating zones may be expected also in numerical experiments.
Figure 1 shows the streamlines in the upper half part of the 4:1 contraction flow and Figure 2 the recirculating zone in the right upper corner.
References:
|
|
|
[Contents] | [Index] |