Collaborator: O. Klein,
P. Philip,
J. Schefter,
J. Sprekels
Cooperation with: Ch. Meyer, A. Rösch, F. Tröltzsch
(Technische Universität Berlin),
K. Böttcher, D. Schulz, D. Siche
(Institut für Kristallzüchtung (IKZ),
Berlin)
Supported by: BMBF: ``Numerische Simulation und Optimierung der
Züchtung von SiC-Einkristallen durch Sublimation aus der Gasphase''
(Numerical simulation and optimization of SiC single crystal growth
by sublimation from the gas phase);
DFG-Forschungszentrum
``Mathematik für Schlüsseltechnologien''
(Research Center ``Mathematics for Key Technologies''), project C9
Description:
![% latex2html id marker 38471
\minipage{0.55\textwidth}\Projektbild {\textwidth}...
...owth apparatus according to [\ref{lit1_sic_Pon}]\label{fig1_sic_1}}
\endminipage](img273.gif) Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large. It is still a challenging problem to grow
sufficiently large SiC crystals with a low defect rate.
Sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method, has been one of
the most successful and most widely used growth techniques of recent
years.
Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large. It is still a challenging problem to grow
sufficiently large SiC crystals with a low defect rate.
Sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method, has been one of
the most successful and most widely used growth techniques of recent
years.
During PVT, a graphite crucible (see Figure 1)
is placed in a low-pressure inert gas
atmosphere consisting of argon. The crucible is then intensely heated,
e.g., by induction heating, to
temperatures up to 3000 K. Inside the crucible,
polycrystalline SiC source powder sublimates, and
the gaseous species diffuse through the cavity from the
powder to the SiC seed.
As the single-crystalline seed is
kept at a temperature below that of the SiC
source, the species crystallize on the seed, which thereby grows into
the reactor.
The physical and mathematical modeling of the growth process leads to a
highly nonlinear system of coupled partial differential equations.
In addition to the kinetics of a rare gas mixture at high temperatures,
one has to consider heat transport by conduction and radiation,
reactive matter transport through porous and granular media, and
different kinds of chemical reactions and phase transitions.
The main control parameters with respect to an optimization of the crystal
growth process are the design of the growth apparatus, the position of the
induction coil, the heating power, and the inert gas pressure.
The heat sources caused by induction heating are computed via an axisymmetric
complex-valued magnetic scalar potential that is determined as the solution
of an elliptic PDE using the imposed voltage as input data. The scalar
potential
enables one to calculate the resulting current density and thus
the heat sources (see [1, 2] and the references
therein).
Within the covered research period, the simulation software
WIAS-HiTNIHS
has been tested at
the IKZ by comparing, for a simple version of the equations, the
results derived with WIAS-HiTNIHS with
results computed by other software. This has led to an enlargement of the
region considered for computations and to some
improvements of WIAS-HiTNIHS.
In [4],
based on the numerical solution of the stationary mathematical model
for the heat transport in the growth system by WIAS-HiTNIHS,
a Nelder-Mead method has been used
for a numerical optimization of
the control parameters frequency f,
power P, and coil position
zrim
for
the radio frequency (RF) induction heating of the growth apparatus.
The control parameters have been determined to minimize
a cost functional, being either
the L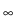 -norm of the radial temperature gradient on
the single crystal surface
or the L2-norm
-norm of the radial temperature gradient on
the single crystal surface
or the L2-norm
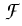 r, 2 of this radial gradient,
or
r, 2 of this radial gradient,
or
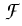 r, 2 minus the L2-norm
r, 2 minus the L2-norm
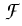 z, 2
of the vertical temperature gradient between SiC source and
seed.
The optimizations have been subject to constraints with respect to a
required temperature difference between source and
seed, a required temperature range at the seed, and an upper bound
for the temperature in the entire apparatus.
z, 2
of the vertical temperature gradient between SiC source and
seed.
The optimizations have been subject to constraints with respect to a
required temperature difference between source and
seed, a required temperature range at the seed, and an upper bound
for the temperature in the entire apparatus.
Several series of Nelder-Mead optimizations of
(P, zrim)
have been performed, varying the used initial values and keeping the
frequency f fixed.
Moreover, also the functional dependence of
the cost functional on
(P, zrim)
as well as the restrictions imposed by the state
constraints
have been studied, varying
the power P and the coil position
zrim and
performing, for each
(P, zrim),
a forward computation to
compute temperature fields
T = T(f, P, zrim)
and the corresponding value of the cost functionals.
Fig. 2:
Contour plots of the functionals
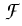 r, 2 (left-hand side)
and
r, 2 (left-hand side)
and
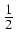
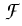 r, 2 -
r, 2 - 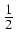
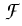 z, 2 (right-hand side)
restricted to the part of the
(P, zrim)-plane where the state constraints
are satisfied.
Therein, a star marks the location where the smallest
value of the considered objective functional
occurred during the series of forward computations discussed,
and the locations of results of 9 corresponding 2-dimensional Nelder-Mead
computations (keeping f = 10 kHz fixed) are
indicated by dots, which can be found
on the lower edge of the respective admissible region.
z, 2 (right-hand side)
restricted to the part of the
(P, zrim)-plane where the state constraints
are satisfied.
Therein, a star marks the location where the smallest
value of the considered objective functional
occurred during the series of forward computations discussed,
and the locations of results of 9 corresponding 2-dimensional Nelder-Mead
computations (keeping f = 10 kHz fixed) are
indicated by dots, which can be found
on the lower edge of the respective admissible region.
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.46\textwidth}{fb03_1_02_sic_fig2.eps.gz}{fb03_1_02_sic_fig3.eps.gz}
\makeatother](img275.gif) |
Moreover, we have performed three-dimensional Nelder-Mead
optimizations, controlling f in addition to P and
zrim.
As in the two-dimensional optimizations, different objective functionals
have been considered. Varying the initial values, series of 27 Nelder-Mead
computations have been performed.
The results for two series are shown in Figure
3.
Fig. 3:
Result values for
(P, zrim, f )
for two series of three-dimensional Nelder-Mead computations,
with a color presentation of the corresponding values
of the objective function
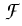 r, 2 (left-hand side)
and
r, 2 (left-hand side)
and
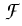 r, 2 -
r, 2 - 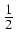
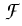 z, 2 (right-hand side).
The big point in each figure corresponds to the triple
with the respective lowest value
of the considered objective function.
z, 2 (right-hand side).
The big point in each figure corresponds to the triple
with the respective lowest value
of the considered objective function.
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.45\textwidth}{fb03_1_02_sic_fig4.eps.gz}{fb03_1_02_sic_fig5.eps.gz}
\makeatother](img276.gif) |
The effect of the respective minimizations of
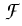 r, 2(T) and of
r, 2(T) and of
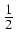
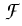 r, 2(T) -
r, 2(T) - 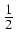
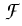 z, 2(T) on
the shape of the temperature distribution between SiC source and
crystal is portrayed in Figure 3.
Therein,
one has the stationary solution for a
generic, unoptimized situation,
and also
the solutions with the lowest values for
z, 2(T) on
the shape of the temperature distribution between SiC source and
crystal is portrayed in Figure 3.
Therein,
one has the stationary solution for a
generic, unoptimized situation,
and also
the solutions with the lowest values for
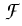 r, 2(T) and for
r, 2(T) and for
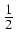
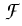 r, 2(T) -
r, 2(T) - 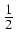
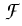 z, 2(T)
found within the three-dimensional Nelder-Mead computations, which
are marked in Figure 3.
z, 2(T)
found within the three-dimensional Nelder-Mead computations, which
are marked in Figure 3.
As a result of the optimizations,
a minimal radial temperature gradient is found to coincide with
a minimal temperature at the single crystal surface, and a maximal
temperature gradient between source and seed is found to coincide
with a low coil position.
In [5], a quite general version of
transient nonlinear and nonlocal heat transport equations has been
discretized using an implicit Euler scheme in time and a finite volume
method in space.
For the corresponding nonlinear and nonlocal discrete scheme,
the existence of a unique discrete solution
has been proved and
discrete L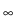 -L1 a priori
estimates have been established.
In [3],
a less general version of the equations has been considered,
and the existence of a unique discrete solution to
the corresponding discrete scheme has been proved under weaker assumptions
for the discretization, and, moreover,
a discrete L
-L1 a priori
estimates have been established.
In [3],
a less general version of the equations has been considered,
and the existence of a unique discrete solution to
the corresponding discrete scheme has been proved under weaker assumptions
for the discretization, and, moreover,
a discrete L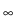 -L
-L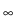 a priori
estimate has been derived.
a priori
estimate has been derived.
Fig. 4:
The shape of the temperature distribution between SiC source and
crystal.
The distribution on the top corresponds to a
generic, unoptimized situation, using f = 10 kHz, P = 10 kW,
and
zrim = 24 cm.
The lower figures present temperature distributions
corresponding to those values for
(f, p, zrim)
with the lowest values for
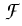 r, 2(T) (left-hand side) and of
r, 2(T) (left-hand side) and of
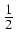
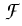 r, 2(T) -
r, 2(T) - 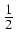
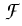 z, 2(T)
(right-hand side)
found by the three-dimensional Nelder-Mead computations,
which have been marked in Figure
3.
z, 2(T)
(right-hand side)
found by the three-dimensional Nelder-Mead computations,
which have been marked in Figure
3.
![\makeatletter
\@DreiProjektbilderNocap[d]{0.49\textwidth}{fb03_1_02_sic_fig6.eps.gz}{fb03_1_02_sic_fig7.eps.gz}{fb03_1_02_sic_fig8.eps.gz}
\makeatother](img277.gif) |
References:
- O. KLEIN, P. PHILIP,
Transient numerical investigation of induction heating during
sublimation growth of silicon carbide single crystals,
J. Crystal Growth, 247 (2002), pp. 219-235.
- ,
Transient temperature phenomena during sublimation growth of silicon
carbide single crystals,
J. Crystal Growth, 249 (2003), pp. 514-522.
- ,
Transient conductive-radiative heat transfer: Discrete existence and
uniqueness for a finite volume scheme,
WIAS Preprint no. 871, 2003.
- C. MEYER, P. PHILIP,
Optimizing the temperature profile during sublimation growth of
SiC single crystals: Control of heating power, frequency, and coil position,
WIAS Preprint no. 895, 2003.
- P. PHILIP,
Transient numerical simulation of sublimation growth of SiC bulk single
crystals. Modeling, finite volume method, results,
Ph.D. thesis,
Humboldt-Universität zu Berlin,
2003,
WIAS Report no. 22, 2003.
- M. PONS, M. ANIKIN, K. CHOUROU,
J.M. DEDULLE, R. MADAR, E. BLANQUET,
A. PISCH, C. BERNARD, P. GROSSE,
C. FAURE, G. BASSET, Y. GRANGE,
State of the art in the modelling of SiC sublimation growth,
Materials Science and Engineering B, 61-62 (1999),
pp. 18-28.
LaTeX typesetting by I. Bremer
2004-08-13
![% latex2html id marker 38471
\minipage{0.55\textwidth}\Projektbild {\textwidth}...
...owth apparatus according to [\ref{lit1_sic_Pon}]\label{fig1_sic_1}}
\endminipage](img273.gif) Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large. It is still a challenging problem to grow
sufficiently large SiC crystals with a low defect rate.
Sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method, has been one of
the most successful and most widely used growth techniques of recent
years.
Owing to numerous technical applications in electronic and
optoelectronic devices,
the industrial demand for high quality silicon carbide (SiC)
bulk single
crystals remains large. It is still a challenging problem to grow
sufficiently large SiC crystals with a low defect rate.
Sublimation growth of SiC bulk single crystals
via physical vapor transport (PVT),
also known as the
modified Lely method, has been one of
the most successful and most widely used growth techniques of recent
years.
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.46\textwidth}{fb03_1_02_sic_fig2.eps.gz}{fb03_1_02_sic_fig3.eps.gz}
\makeatother](img275.gif)
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.45\textwidth}{fb03_1_02_sic_fig4.eps.gz}{fb03_1_02_sic_fig5.eps.gz}
\makeatother](img276.gif)
![\makeatletter
\@DreiProjektbilderNocap[d]{0.49\textwidth}{fb03_1_02_sic_fig6.eps.gz}{fb03_1_02_sic_fig7.eps.gz}{fb03_1_02_sic_fig8.eps.gz}
\makeatother](img277.gif)