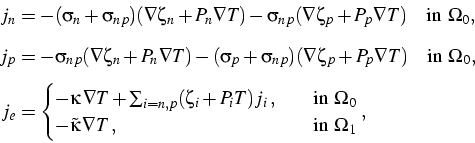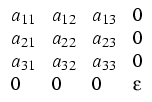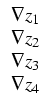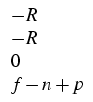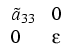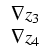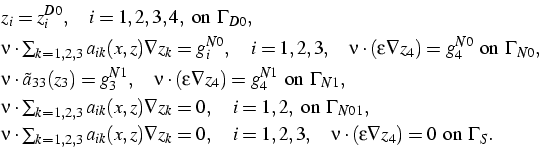Collaborator: A. Glitzky,
R. Hünlich
Cooperation with: L. Recke (Humboldt-Universität zu Berlin)
Description:
 Semiconductor devices are heterostructures
consisting of
various materials (different semiconducting materials,
passive layers, and metals as contacts, for example).
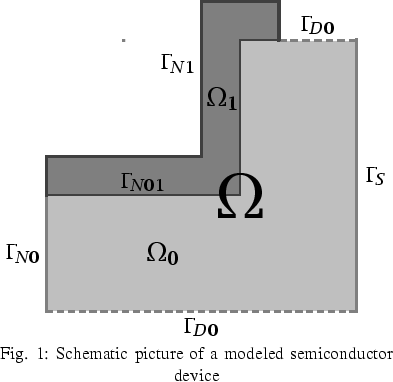
A typical situation is shown in
Figure 1.
Equations for the contacts are substituted
by Dirichlet boundary conditions on the two parts of the boundary
Semiconductor devices are heterostructures
consisting of
various materials (different semiconducting materials,
passive layers, and metals as contacts, for example).
A typical situation is shown in
Figure 1.
Equations for the contacts are substituted
by Dirichlet boundary conditions on the two parts of the boundary
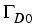 .
In the remaining domain
.
In the remaining domain 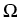 , involving
the passive layer (
, involving
the passive layer (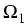 ) and semiconducting materials (
) and semiconducting materials (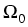 ),
we have to formulate a Poisson equation
and an energy balance equation
with boundary conditions on
),
we have to formulate a Poisson equation
and an energy balance equation
with boundary conditions on
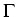 =
= 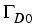
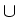
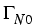
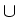
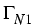
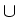
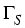 , where the subscripts D, N,
and S indicate the parts
with Dirichlet, inhomogeneous Neumann, and symmetry boundary conditions,
respectively. Only in the part
, where the subscripts D, N,
and S indicate the parts
with Dirichlet, inhomogeneous Neumann, and symmetry boundary conditions,
respectively. Only in the part
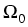 , continuity equations for electrons
and holes have to be taken into account, and here we must formulate
boundary conditions on
, continuity equations for electrons
and holes have to be taken into account, and here we must formulate
boundary conditions on
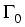 =
= 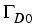
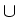
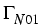
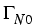
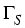 .
.
Let T and 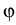 denote the lattice
temperature and the electrostatic potential. Then
the state equations for electrons and holes are given by
the following expressions
denote the lattice
temperature and the electrostatic potential. Then
the state equations for electrons and holes are given by
the following expressions
n =
N(
. ,
T)
F
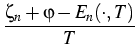
,
p =
P(
. ,
T)
F
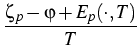
in
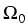
,
where n and p are the electron
and hole densities, N and P are the effective densities of state,
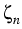 and
and 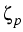 are the electrochemical
potentials,
En and Ep are the energy band edges, respectively.
The function F arises from
a distribution function (e.g.,
F(y) = e y in the case of
Boltzmann statistics, or
F(y) =
are the electrochemical
potentials,
En and Ep are the energy band edges, respectively.
The function F arises from
a distribution function (e.g.,
F(y) = e y in the case of
Boltzmann statistics, or
F(y) = 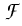 1/2(y)
in the case of Fermi-Dirac statistics).
The electrostatic potential
1/2(y)
in the case of Fermi-Dirac statistics).
The electrostatic potential 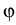 fulfils the Poisson equation
Here,
fulfils the Poisson equation
Here,
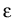 is the dielectric permittivity and
f is a given doping profile.
Mixed boundary conditions on
is the dielectric permittivity and
f is a given doping profile.
Mixed boundary conditions on 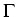 have to be prescribed.
For the densities of the particle fluxes
jn, jp and of the total energy flux je,
we make the ansatz (see [1])
with conductivities
have to be prescribed.
For the densities of the particle fluxes
jn, jp and of the total energy flux je,
we make the ansatz (see [1])
with conductivities
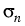 =
= 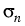 (x, n, p, T) > 0,
(x, n, p, T) > 0, 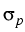 =
= 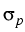 (x, n, p, T) > 0,
(x, n, p, T) > 0,
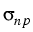 =
= 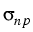 (x, n, p, T)
(x, n, p, T)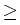 0,
0,
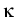 =
= 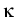 (x, n, p, T) > 0,
(x, n, p, T) > 0,
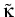 =
= 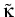 (x, T) > 0, and
transported entropies
Pn = Pn(x, n, p, T), Pp = Pp(x, n, p, T).
These flux densities fulfil the balance equations
(x, T) > 0, and
transported entropies
Pn = Pn(x, n, p, T), Pp = Pp(x, n, p, T).
These flux densities fulfil the balance equations
 . jn = - R, . jn = - R, . jp = - Rin . jp = - Rin 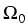 , , . je = 0in . je = 0in 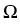 , ,
|
(2) |
where the net recombination rate R has the form
R =
r(
. ,
n,
p,
T)(e
(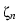 +
+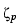 )/T
)/T -1)in
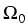
.
Suitable boundary conditions on 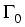 for
the first two continuity equations and on
for
the first two continuity equations and on 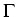 for the last energy balance equation
have to be added.
for the last energy balance equation
have to be added.
We use the variables
z = (z1, z2, z3, z4) = (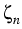 /T|
/T|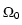 ,
,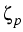 /T|
/T|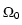 , -1/T,
, -1/T,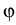 ), where
z1, z2 are defined on
), where
z1, z2 are defined on 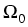 , while z3, z4 live on
, while z3, z4 live on 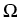 .
Then the stationary energy model for semiconductor
devices can be written in the more compact form
.
Then the stationary energy model for semiconductor
devices can be written in the more compact form
with
coefficient functions
aik(x, z) = aki(x, z), x 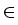
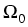 , z
, z 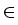
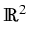 x (-
x (- 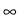 , 0) x
, 0) x 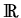 ,
i, k = 1,..., 3,
,
i, k = 1,..., 3,
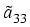 (x, z3),
x
(x, z3),
x 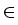
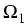 ,
z3
,
z3 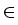 (-
(- 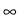 , 0),
, 0),
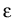 (x), x
(x), x 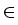
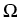 , and R, n, and p have to be regarded as
functions of
x
, and R, n, and p have to be regarded as
functions of
x 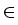
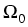 and
z
and
z 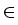
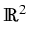 x (-
x (- 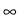 , 0) x
, 0) x 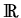 .
.
We consider the boundary conditions
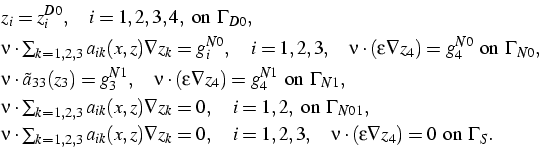
|
(4) |
We use the vectors
zD = (zD1,..., zD4),
g = (g1N0,..., g4N0, g3N1, g4N1), and the triplet
of data
w = (zD, g, f )
and look for weak solutions of (3), (4)
in the form
z = Z + zD, where zD corresponds to a function
fulfilling the Dirichlet boundary conditions and Z represents the
homogeneous part of the solution.
We assume that
the boundary values ziD, i = 1, 2, 3, 4, are traces of
W1, p-functions, p > 2.
Under weak assumptions on the coefficient functions aij,
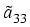 , and
, and
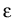 (for example,
(for example,  can be composed of different
semiconducting
materials), we found
W1, q-formulations
(q
can be composed of different
semiconducting
materials), we found
W1, q-formulations
(q 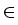 (2, p]) for that system of equations,
(2, p]) for that system of equations,
If
w* = (zD*, g*, f*) is arbitrarily given such that
the boundary values ziD*, i = 1, 2, 3,
are constants,
zD*1 + zD*1 = 0 and
zD*3 < 0
and
g* = (0, 0, 0, g4N0*, 0, g4N1*),
then there exists a unique solution Z* of
F(Z*, w*) = 0. Then
z* = Z* + zD* is a thermodynamic equilibrium
of (3), (4).
Using techniques from [5], the operator F turned out to be
continuously differentiable. For suitable q > 2,
we proved that its linearization
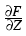 (Z*, w*)
is an injective
Fredholm operator of index zero.
For this purpose we derived new results concerning W1, q-regularity
and
surjectivity for strongly coupled systems of linear elliptic equations
which are defined on different domains.
Here we adapted ideas of [4].
We applied the Implicit Function Theorem
and obtained that
for
w = (zD, g, f ) near w*, the equation
F(Z, w) = 0 has a unique solution Z near
Z*. Thus, near z* there
is a locally unique Hölder continuous solution z = Z + zD
of (3), (4).
For details and the precise assumptions of our investigations see
[3].
(Z*, w*)
is an injective
Fredholm operator of index zero.
For this purpose we derived new results concerning W1, q-regularity
and
surjectivity for strongly coupled systems of linear elliptic equations
which are defined on different domains.
Here we adapted ideas of [4].
We applied the Implicit Function Theorem
and obtained that
for
w = (zD, g, f ) near w*, the equation
F(Z, w) = 0 has a unique solution Z near
Z*. Thus, near z* there
is a locally unique Hölder continuous solution z = Z + zD
of (3), (4).
For details and the precise assumptions of our investigations see
[3].
In [2]
we investigated an energy model with multiple species, but there
the continuity equations, the energy balance equation, and
the Poisson equation were defined on the same domain.
References:
- G. ALBINUS, H. GAJEWSKI, R. HÜNLICH,
Thermodynamic design of energy models of
semiconductor devices,
Nonlinearity, 15 (2002),
pp. 367-383.
- A. GLITZKY, R. HÜNLICH,
Stationary solutions of two-dimensional heterogeneous
energy models with multiple species,
WIAS Preprint no. 896, 2003, to appear in: Banach Cent. Publ.
- , Stationary solutions of a two-dimensional heterogeneous energy
model for semiconductor devices near equilibrium,
in preparation.
- K. GRÖGER,
A W1, p-estimate for solutions to mixed boundary value problems
for second order elliptic differential equations,
Math. Ann., 283 (1989), pp. 679-687.
-
L. RECKE,
Applications of the implicit function theorem to
quasi-linear elliptic boundary value problems with non-smooth data,
Commun. Partial Differ. Equations, 20 (1995), pp. 1457-1479.
LaTeX typesetting by I. Bremer
2004-08-13
 Semiconductor devices are heterostructures
consisting of
various materials (different semiconducting materials,
passive layers, and metals as contacts, for example).
A typical situation is shown in
Figure 1.
Equations for the contacts are substituted
by Dirichlet boundary conditions on the two parts of the boundary
Semiconductor devices are heterostructures
consisting of
various materials (different semiconducting materials,
passive layers, and metals as contacts, for example).
A typical situation is shown in
Figure 1.
Equations for the contacts are substituted
by Dirichlet boundary conditions on the two parts of the boundary
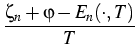
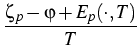
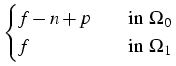 .
.