Thermodynamics-based modeling of semiconductor lasers
Collaborator: U. Bandelow,
H. Gajewski,
R. Hünlich
Cooperation with: H. Wenzel (Ferdinand-Braun-Institut für
Höchstfrequenztechnik (FBH) Berlin)
Description:
In modern semiconductor devices
such as high power transistors or
lasers, thermal effects caused by strong electric and optical fields
and by strong recombination play an important role and have to be included
in the mathematical models.
Indeed, there is a large variety of energy models for semiconductor devices.
Typically, these models base on the usual state equations and continuity
equations for the carrier densities, and on the balance of the total energy expressed by the equation
for the density u and the current density ju
of this total energy, where 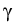 counts for the radiation which
is emitted from the device.
Furthermore, differential relations for u and general thermodynamic
relations for ju are used to transform the energy balance equation
(1) into a heat flow equation
where ch is the heat capacity and
counts for the radiation which
is emitted from the device.
Furthermore, differential relations for u and general thermodynamic
relations for ju are used to transform the energy balance equation
(1) into a heat flow equation
where ch is the heat capacity and 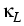 the heat conductivity.
While the heat flow equation
(2) with the description
of the source term H is well established, the discussion about its
relation to the conservation law of energy is still ongoing.
the heat conductivity.
While the heat flow equation
(2) with the description
of the source term H is well established, the discussion about its
relation to the conservation law of energy is still ongoing.
In our model, the transport of electrons and holes is ruled by the
drift-diffusion equations
-  ( (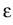  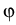 ) ) |
= |
C + p - n , |
(3) |
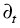 n - n -  . . 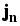 = - R , = - R , |
|
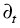 p + p +  . . 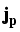 = - R = - R |
(4) |
for the densities of electrons n and holes p, and the electrostatic
potential 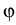 in the transverse cross section
in the transverse cross section 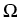 of the laser.
The recombination rate R in (4) involves
all non-radiative and radiative recombination processes.
The current densities
of the laser.
The recombination rate R in (4) involves
all non-radiative and radiative recombination processes.
The current densities
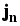 and
and
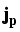 are driven by the
gradients of the quasi-Fermi potentials fn and fp, which
are linked with the carrier concentrations by means of Fermi-Dirac
statistics:
are driven by the
gradients of the quasi-Fermi potentials fn and fp, which
are linked with the carrier concentrations by means of Fermi-Dirac
statistics:
n = Nc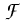 1/2 1/2 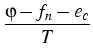  , p = Nv , p = Nv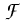 1/2 1/2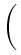 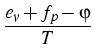 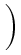 . .
|
(5) |
The optical field distribution
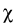 (
(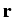 ) within
) within 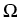 is governed by the waveguide equation
where the optical response function
is governed by the waveguide equation
where the optical response function
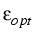 (
(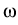 ,
,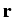 )
contains the refractive index and the material gain, which depends on almost
all properties of the device and its operating state,
in particular on n, p, and T.
The respective (complex) eigenvalue
)
contains the refractive index and the material gain, which depends on almost
all properties of the device and its operating state,
in particular on n, p, and T.
The respective (complex) eigenvalue 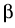 readily counts the number Ns
of photons in the laser by a corresponding photon rate equation
readily counts the number Ns
of photons in the laser by a corresponding photon rate equation
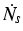 = vg(2 = vg(2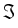 m m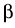 - - 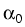 - - 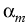 )Ns + rsp. )Ns + rsp.
|
(7) |
The field intensity
Ns . |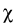 (
(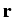 )|2 times the material gain
enters the radiative recombination rate in R in
(4), which self-consistently completes our model
([1]).
Based on an expression for the density of the free energy
)|2 times the material gain
enters the radiative recombination rate in R in
(4), which self-consistently completes our model
([1]).
Based on an expression for the density of the free energy
| f |
= |
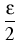 | | 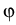 |2 + cLT(1 - logT) + urad - Tsrad |2 + cLT(1 - logT) + urad - Tsrad |
|
| |
|
+ n[T(log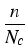 -1) + ec] + p[T(log -1) + ec] + p[T(log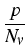 -1) - ev], -1) - ev], |
(8) |
we extended (3)-(7) to a thermodynamics-based system
(2)-(7)
of evolution equations for semiconductor lasers in a deductive way.
Here, we only apply first principles like the entropy maximum principle
and the principle of partial local equilibrium as well as the Onsager
symmetry relations ([2]).
In particular we could show that the heat source term H in (2) is
| H |
= |
T Pn . Pn . 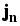 - T - T Pp . Pp . 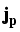 + T + T . ( . (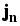 - - 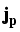 ) ) |
|
| |
|
- 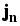 . ( . ( fn - Pn fn - Pn T) - T) - 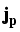 . ( . ( fp + Pp fp + Pp T) T) |
|
| |
|
+ (un + up)R - 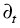 urad - urad - 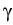 , , |
(9) |
with the thermoelectric powers Pn, Pp, and the energy density of
the optical field
urad = 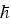
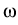 |
|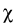 |2Ns.
The current densities
|2Ns.
The current densities
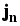 and
and
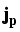 are now driven by the
gradients of the temperature T, too.
Moreover, a continuity equation for the entropy density s
with the entropy current density
are now driven by the
gradients of the temperature T, too.
Moreover, a continuity equation for the entropy density s
with the entropy current density
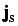 could be derived.
The dissipation rate d
could be derived.
The dissipation rate d
| d |
= |
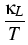 | | T|2 + T|2 + 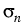 | | fn - Pn fn - Pn T|2 + T|2 + 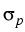 | | fp + Pp fp + Pp T|2 T|2 |
|
| |
|
+ 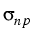 | | (fn - fp) - (Pn + Pp) (fn - fp) - (Pn + Pp) T|2 + (fp - fn)R - T|2 + (fp - fn)R - 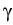 |
(11) |
appears to be always positive for a device which is isolated from the outside
world (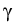 = 0).
Therefore, by partial integration of (10) and supposing no-flux
boundary conditions,
and
= 0).
Therefore, by partial integration of (10) and supposing no-flux
boundary conditions,
and 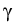 = 0, it follows, according to the second law of thermodynamics,
In conclusion, as a feature, we are able to prove the thermodynamic correctness
of our model in view of the second law of thermodynamics (12).
= 0, it follows, according to the second law of thermodynamics,
In conclusion, as a feature, we are able to prove the thermodynamic correctness
of our model in view of the second law of thermodynamics (12).
The complete energy transport model
has been implemented in WIAS-TeSCA
([3]), a numerical code for the simulation of semiconductor devices.
On this base, we have demonstrated the simulation of long-wavelength
edge-emitting quantum well lasers, with a special focus on the self-heating
of the device and the modulation response ([2]).
References:
- U. BANDELOW, TH. KOPRUCKI, R. HÜNLICH,
Simulation of static and dynamic properties of
edge-emitting multi quantum well lasers,
IEEE J. Select. Topics Quantum Electron.,
9 (2003), pp. 798-806.
- U. BANDELOW, H. GAJEWSKI, R. HÜNLICH,
Thermodynamics-based modeling of edge-emitting quantum well lasers,
in preparation.
- WIAS-TeSCA.
http://www.wias-berlin.de/software/tesca, 2003.
LaTeX typesetting by I. Bremer
2004-08-13