- Modellierung von verzerrbaren porösen Körpern,
- Mikro-Makro- und Phasenübergänge.
- 1.
- Lineare Stabilität von stationären Strömungen in poroelastischen
Materialien. Es wurde bewiesen, dass nur eine 2D-Störung mit
Massenaustausch eine Instabilität der 1D-Strömung erzeugen kann. Der
Bereich der Stabilität ist von drei Materialparametern abhängig:
Durchlässigkeit des Körpers, Durchlässigkeit des Randes und innere
Fläche der Kanäle des Körpers.
- 2.
- Ausbreitung von linearen Schallwellen in gesättigten porösen
Körpern. Schwerpunktmäßig wurde der Bereich niedriger Frequenzen und
langer Wellen untersucht. Für Oberflächenwellen wurden Körper mit
undurchlässigen Rändern erforscht. Es wurde bewiesen, dass für
Anfangswertaufgaben (d. h. Wellenzahl k ist reell) der Bereich langer
Wellen mit k<kcr, kcr - eine kritische Wellenzahl, für die
Ausbreitung von P2-Wellen verboten ist. Gleichzeitig wurde bewiesen,
dass in Randwertaufgaben (d. h. Frequenz
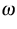ist reell) die
Wellenausbreitung sich im gesamten Frequenzbereich 
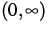regulär verhält. Diese Eigenschaften beeinflussen die
Ausbreitungsbedingungen für Oberflächenwellen, die auch untersucht
wurden.
- 1.
- Linear stability of stationary flows in poroelastic materials. It was
proven that solely a 2D disturbance with mass exchange can yield an
instability in 1D flow. The range of stability depends on three material
parameters: bulk permeability, surface permeability and internal surface of
channels of the medium.
- 2.
- Propagation of linear acoustic
waves in saturated porous bodies. Primarily the range of low
frequencies and long waves was investigated. For the case of surface
waves bodies with impermeable boundaries were
considered. It has been proven that for initial value problems
(i.e. the wave number k is real) a range of long waves, k<kcr,
limited by a critical value of the wave
number kcr is forbidden for P2 waves. Simultaneously
it has been proven that for boundary value problems (i.e. the
frequency 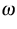is real) the propagation of waves is regular in
the whole range of frequencies 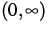. These
properties influence the propagation conditions for surface
waves, which have been
investigated as well.
- 3.
- Thermodynamische Grundlagen der Modellbildung für gesättigte thermoporoelastische Körper. Es wurde gezeigt, dass die klassische Biot'sche Theorie als ein Grenzfall des Modells mit konstitutiver Abhängigkeit vom Gradienten der Porosität folgt. Für diese makroskopische Modellbildung wurde auch eine systematische Mikro-Makro-Methode zur Berechnung mancher Materialparameter (Kompressibilitäten) entwickelt, die als Sonderfall die klassischen Gassmann-Formeln ergibt.
Auf dem Gebiet der Mikro-Makro-Übergänge
wurden die folgenden vier Problemstellungen behandelt:
- Phasenübergänge, zum Teil gefördert im
BMBF-Programm Neue Mathematische Verfahren in Industrie und
Dienstleistungen unter 03DRM3B5
Zurzeit werden hier zwei unterschiedliche Phänomene behandelt: Morphologieänderungen auf der
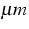-Skala von Lotmaterialien der
Mikroelektronik und Phasenübergänge mit Tropfenbildung auf der
mm-Skala in Wafermaterialien für optoelektronische Anwendungen.
- Mehrskalenmodellierung von thermoelastischen Körpern und Mikro-Makro-Übergänge in der atomaren Kette für verschiedene Skalierungen, gefördert im DFG-Schwerpunktprogramm SPP 1095 ,,Analysis, Modellbildung und Simulation von Mehrskalenproblemen``
- Kinetische Behandlung von ausgewählten Anfangs- und Randwertproblemen für hyperbolische Systeme und kinetische Gleichungen, gefördert im DFG-Schwerpunktprogramm ,,ANumE -- Analysis und Numerik von Erhaltungsgleichungen``
- Die Spannungsanalyse von dünnen einkristallinen Wafern wurde als rein industrielle Anwendung im Berichtszeitraum wieder aufgenommen.
- 3.
- Thermodynamic foundations of modeling of saturated poroelastic bodies. It has been shown that the classical Biot theory is a limit case of a general model which contains a constitutive dependence on the gradient of porosity. For this macroscopic modeling a systematic micro-macro method of evaluation of some material parameters (compressibilities) has been developed. The classical Gassmann relations become a special case of this method.
Within the area of micro-macro
transitions, the research group
``Continuum Mechanics'' has considered four different fields of
problems.
- Phase transitions, partly funded within
the BMBF program New Mathematical Methods in Industry and
Services under the contract 03DRM3B5
Currently, two different phenomena are studied: morphological changes on the
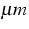scale of solder
materials that are used in microelectronic
devices and phase transitions including the formation of
droplets on
the mm scale of wafer material that is used in optoelectronic
applications.
- Multi-scale modeling of thermoelastic bodies and Micro-macro transitions of the atomic chain for various scalings, funded within the DFG Priority Program SPP 1095 ``Analysis, Modeling and Simulation of Multiscale Problems''
- Kinetic treatment of selected initial and boundary value problems of hyperbolic systems and kinetic equations, funded within the DFG Priority Program ``ANumE -- Analysis and Numerics of Conservation Laws''
- Stress analysis of thin single crystal wafers--a purely industrial study--was restarted.
Die Studie über Mehrskalenmodellierung ist ein Gemeinschaftsprojekt mit J. Sprekels und eine Kooperation mit A. Mielke (Universität Stuttgart). Am Beispiel der atomaren Kette wird für verschiedene Skalierungen die Möglichkeit rigoroser Mikro-Makro-Übergänge untersucht. Durch die Kooperation mit A. Mielke hat sich ein neuer Zugang ergeben, der die am WIAS gefundene mikroskopische Oszillatorbewegung zu allgemeinen mehrparametrigen Traveling-Wave-Lösungen der Newton'schen Bewegungsgleichungen in Beziehung setzt.
The study on multiscale modeling is a joint project with J. Sprekels and a collaboration with A. Mielke (Universität Stuttgart). The atomic chain serves as an example, where the possibility of rigorous micro-macro transitions for various scalings is discussed. Due to the collaboration with A. Mielke, a new aspect is introduced that relates the microscopic oscillator motion, which was previously observed at WIAS, to general multi-parametric traveling-wave solutions of Newton's equations of motion.
Aufgrund industrieller Nachfrage wurde das Projekt Spannungsanalyse von dünnen Platten wieder aufgenommen, um folgende Ziele zu erreichen: 1. Umwandlung des WIAS-Codes, welcher die von Kármán'schen Plattengleichungen implementiert, in kommerziell nutzbare Software. 2. Bestimmung der Zuverlässigkeit von Plattentheorien in Bezug auf das ursprüngliche 3D-Elastizitätsproblem.
Due to industrial request, the project on Stress analysis of thin plates is reconsidered in order to reach the following objectives: (1) Transformation of the WIAS code, that solves the von Kármán plate system, into a commercially usable software tool. (2) Determination of the reliability of plate theories with respect to the original 3D elasticity problem.