Each facet is a polygonal region, it may have any number of sides and may be non-convex, possibly with holes, segments and vertices in it. A facet can represent any planar straight line graph (PSLG), which is a popular input model used by many two-dimensional mesh algorithms. A facet is actually a PSLG embedded in three dimensions. An example is given in the above figure, the shaded area highlights a facet.

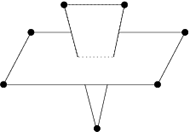
PLCs have restrictions like any other complex. For a PLC X, the elements of X must be closed under intersection. For example, two segments only can intersect at a common vertex which is also in X. Two facets of X may intersect only at a shared segment or vertex or a union of shared segments and vertices (because facets are non-convex). The following figures show non-closed configurations for examples.

Another restriction of the facets of PLCs is that the point set which used to define a facet must be coplanar.

Any polyhedron is a PLC. Furthermore, PLCs are more flexible than polyhedra to represent three-dimensional geometric objects. For example, the shaded facet in the above figure can not be represented by any polygon. For domains having curved surfaces (which are not piecewise linear), the surface triangulations are previously required, hence, PLCs can approximately represent any three-dimensional domain. Following are some examples of PLCs represented by surface meshes.