One focus of our research on financial models is the development and analysis of rough volatility models. Here, the stochastic volatility is given by a fractional process, such as fractional Brownian motion with a Hurst index smaller than ½. Such models allow high accuracy in the representation of derivative prices as well as high statistical accuracy for price time series. On the other hand, rough volatility models are not Markov processes, and accordingly challenges arise in simulating the processes as well as computing derivative prices.
Another research focus in the past has been interest rate modeling with multi-curve models and FX EurIBOR models.
Highlights
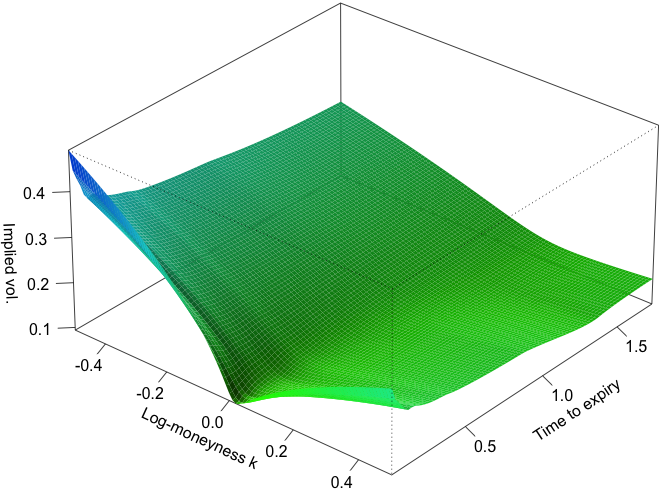
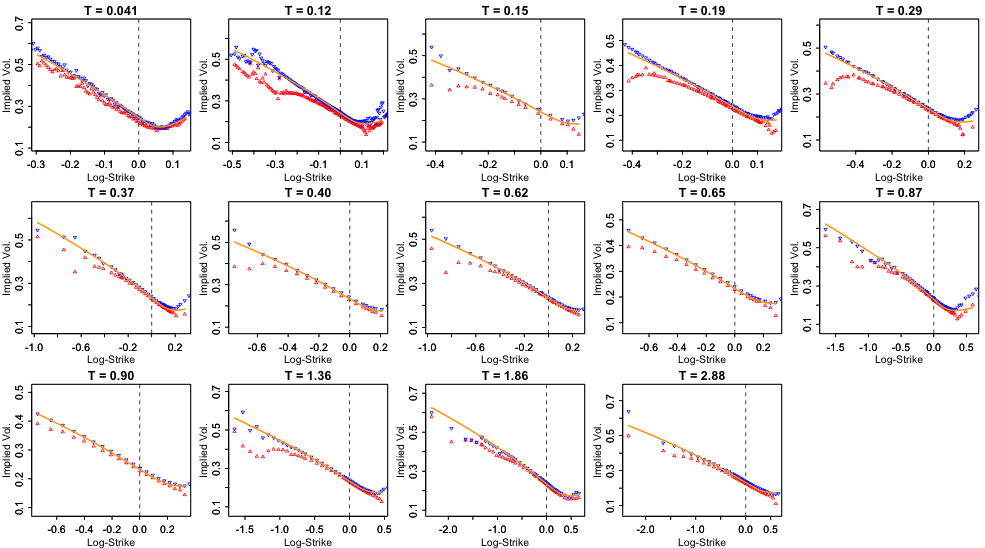
WIAS employees played a leading role in establishing rough volatility models, which are increasingly proving to be a new paradigm in modeling stock markets. The so-called rough Bergomi model in particular provides a precise match with market data of both implied volatilities and realized variances. It is the first model of its kind to accurately capture the skew of implied volatility, even for very short option maturities. Nevertheless, this model is described by a very small number of free parameters and is therefore very robust. At the institute, a number of new methods for derivative pricing in rough Bergomi model and similar rough volatility models have been developed, including precise asymptotic price formulas and accurate numerical simulation methods. In addition, new theoretical frameworks for analyzing rough volatility models have been developed using the theory of regularity structures.In a more general context, new methods have been developed for calibrating general stochastic volatility models using tools from the theory of RKHS.
Publications
 Monographs
Monographs
-
D. Belomestny, J. Schoenmakers, Advanced Simulation-Based Methods for Optimal Stopping and Control: With Applications in Finance, Macmillan Publishers Ltd., London, 2018, 364 pages, (Monograph Published), DOI 10.1057/978-1-137-03351-2 .
-
CH. Bayer, J.G.M. Schoenmakers, Option Pricing in Affine Generalized Merton Models, in: Advanced Modelling in Mathematical Finance -- In Honour of Ernst Eberlein, J. Kallsen, A. Papapantoleon , eds., Springer Proceedings in Mathematics & Statistics, Springer International Publishing Switzerland, Cham, 2016, pp. 219--239, (Chapter Published).
Abstract
In this article we consider affine generalizations of the Merton jump diffusion model Merton (1976) and the respective pricing of European options. On the one hand, the Brownian motion part in the Merton model may be generalized to a log-Heston model, and on the other hand, the jump part may be generalized to an affine process with possibly state dependent jumps. While the characteristic function of the log-Heston component is known in closed form, the characteristic function of the second component may be unknown explicitly. For the latter component we propose an approximation procedure based on the method introduced in Belomestny, Kampen, Schoenmakers (2009). We conclude with some numerical examples. -
J.G.M. Schoenmakers, Chapter 12: Coupling Local Currency Libor Models to FX Libor Models, in: Recent Developments in Computational Finance, Th. Gerstner, P. Kloeden, eds., 14 of Interdisciplinary Mathematical Sciences, World Scientific Publishers, Singapore, 2013, pp. 429--444, (Chapter Published).
-
J.G.M. Schoenmakers, Robust Libor Modelling and Pricing of Derivative Products, Chapman & Hall CRC Press, 2005, 202 pages, (Monograph Published).
 Articles in Refereed Journals
Articles in Refereed Journals
-
CH. Bayer, Ch. Ben Hammouda, A. Papapantoleon, M. Samet, R. Tempone, Optimal damping with hierarchical adaptive quadrature for efficient Fourier pricing of multi-asset options in Lévy models, Journal of Computational Finance, 27 (2023), pp. 43--86, DOI 10.21314/JCF.2023.012 .
Abstract
Efficient pricing of multi-asset options is a challenging problem in quantitative finance. When the characteristic function is available, Fourier-based methods become competitive compared to alternative techniques because the integrand in the frequency space has often higher regularity than in the physical space. However, when designing a numerical quadrature method for most of these Fourier pricing approaches, two key aspects affecting the numerical complexity should be carefully considered: (i) the choice of the damping parameters that ensure integrability and control the regularity class of the integrand and (ii) the effective treatment of the high dimensionality. To address these challenges, we propose an efficient numerical method for pricing European multi-asset options based on two complementary ideas. First, we smooth the Fourier integrand via an optimized choice of damping parameters based on a proposed heuristic optimization rule. Second, we use sparsification and dimension-adaptivity techniques to accelerate the convergence of the quadrature in high dimensions. Our extensive numerical study on basket and rainbow options under the multivariate geometric Brownian motion and some Lévy models demonstrates the advantages of adaptivity and our damping rule on the numerical complexity of the quadrature methods. Moreover, our approach achieves substantial computational gains compared to the Monte Carlo method. -
CH. Bayer, M. Eigel, L. Sallandt, P. Trunschke, Pricing high-dimensional Bermudan options with hierarchical tensor formats, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 14 (2023), pp. 383--406, DOI 10.1137/21M1402170 .
-
CH. Bayer, S. Breneis, Markovian approximations of stochastic Volterra equations with the fractional kernel, Quantitative Finance, 23 (2023), pp. 53--70 (published online on 24.11.2022), DOI 10.1080/14697688.2022.2139193 .
Abstract
We consider rough stochastic volatility models where the variance process satisfies a stochastic Volterra equation with the fractional kernel, as in the rough Bergomi and the rough Heston model. In particular, the variance process is therefore not a Markov process or semimartingale, and has quite low Hölder-regularity. In practice, simulating such rough processes thus often results in high computational cost. To remedy this, we study approximations of stochastic Volterra equations using an N-dimensional diffusion process defined as solution to a system of ordinary stochastic differential equation. If the coefficients of the stochastic Volterra equation are Lipschitz continuous, we show that these approximations converge strongly with superpolynomial rate in N. Finally, we apply this approximation to compute the implied volatility smile of a European call option under the rough Bergomi and the rough Heston model. -
CH. Bayer, M. Fukasawa, S. Nakahara, Short communication: On the weak convergence rate in the discretization of rough volatility models, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 13 (2022), pp. SC66--SC73, DOI 10.1137/22M1482871 .
-
CH. Bayer, J. Qiu, Y. Yao, Pricing options under rough volatility with backward SPDEs, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 13 (2022), pp. 179--212, DOI 10.1137/20M1357639 .
Abstract
In this paper, we study the option pricing problems for rough volatility models. As the framework is non-Markovian, the value function for a European option is not deterministic; rather, it is random and satisfies a backward stochastic partial differential equation (BSPDE). The existence and uniqueness of weak solutions is proved for general nonlinear BSPDEs with unbounded random leading coefficients whose connections with certain forward-backward stochastic differential equations are derived as well. These BSPDEs are then used to approximate American option prices. A deep learning-based method is also investigated for the numerical approximations to such BSPDEs and associated non-Markovian pricing problems. Finally, the examples of rough Bergomi type are numerically computed for both European and American options. -
C. Bellingeri, A. Djurdjevac, P. Friz, N. Tapia, Transport and continuity equations with (very) rough noise, SN Partial Differential Equations and Applications, 2 (2021), pp. 2--26, DOI 10.1007/s42985-021-00101-y .
Abstract
Existence and uniqueness for rough flows, transport and continuity equations driven by general geometric rough paths are established. -
M. Redmann, Ch. Bayer, P. Goyal, Low-dimensional approximations of high-dimensional asset price models, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 12 (2021), pp. 1--28, DOI 10.1137/20M1325666 .
Abstract
We consider high-dimensional asset price models that are reduced in their dimension in order to reduce the complexity of the problem or the effect of the curse of dimensionality in the context of option pricing. We apply model order reduction (MOR) to obtain a reduced system. MOR has been previously studied for asymptotically stable controlled stochastic systems with zero initial conditions. However, stochastic differential equations modeling price processes are uncontrolled, have non-zero initial states and are often unstable. Therefore, we extend MOR schemes and combine ideas of techniques known for deterministic systems. This leads to a method providing a good pathwise approximation. After explaining the reduction procedure, the error of the approximation is analyzed and the performance of the algorithm is shown conducting several numerical experiments. Within the numerics section, the benefit of the algorithm in the context of option pricing is pointed out. -
CH. Bayer, F. Harang, P. Pigato, Log-modulated rough stochastic volatility models, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 12 (2021), pp. 1257--1284, DOI 10.1137/20M135902X .
Abstract
We propose a new class of rough stochastic volatility models obtained by modulating the power-law kernel defining the fractional Brownian motion (fBm) by a logarithmic term, such that the kernel retains square integrability even in the limit case of vanishing Hurst index H. The so-obtained log-modulated fractional Brownian motion (log-fBm) is a continuous Gaussian process even for H = 0. As a consequence, the resulting super-rough stochastic volatility models can be analysed over the whole range of Hurst indices between 0 and 1/2, including H = 0, without the need of further normalization. We obtain the usual power law explosion of the skew as maturity T goes to 0, modulated by a logarithmic term, so no flattening of the skew occurs as H goes to 0. -
P. Friz, P. Gassiat, P. Pigato, Precise asymptotics: Robust stochastic volatility models, The Annals of Applied Probability, 31 (2021), pp. 896--940, DOI 10.1214/20-AAP1608 .
Abstract
We present a new methodology to analyze large classes of (classical and rough) stochastic volatility models, with special regard to short-time and small noise formulae for option prices. Our main tool is the theory of regularity structures, which we use in the form of Bayer et al. (Math. Finance30 (2020) 782--832) In essence, we implement a Laplace method on the space of models (in the sense of Hairer), which generalizes classical works of Azencott and Ben Arous on path space and then Aida, Inahama--Kawabi on rough path space. When applied to rough volatility models, for example, in the setting of Bayer, Friz and Gatheral (Quant. Finance16 (2016) 887--904) and Forde--Zhang (SIAM J. Financial Math.8 (2017) 114--145), one obtains precise asymptotics for European options which refine known large deviation asymptotics. -
P. Friz, P. Gassiat, P. Pigato, Short-dated smile under rough volatility: Asymptotics and numerics, Quantitative Finance, 22 (2022), pp. 463--480 (published online on 07.12.2021), DOI 10.1080/14697688.2021.1999486 .
Abstract
In Friz et al. [Precise asymptotics for robust stochastic volatility models. Ann. Appl. Probab, 2021, 31(2), 896?940], we introduce a new methodology to analyze large classes of (classical and rough) stochastic volatility models, with special regard to short-time and small-noise formulae for option prices, using the framework [Bayer et al., A regularity structure for rough volatility. Math. Finance, 2020, 30(3), 782?832]. We investigate here the fine structure of this expansion in large deviations and moderate deviations regimes, together with consequences for implied volatility. We discuss computational aspects relevant for the practical application of these formulas. We specialize such expansions to prototypical rough volatility examples and discuss numerical evidence. -
CH. Bayer, Ch.B. Hammouda, R. Tempone, Hierarchical adaptive sparse grids and quasi-Monte Carlo for option pricing under the rough Bergomi model, Quantitative Finance, published online on 20.04.2020, urlhttps://doi.org/10.1080/14697688.2020.1744700, DOI 10.1080/14697688.2020.1744700 .
Abstract
The rough Bergomi (rBergomi) model, introduced recently in Bayer et al. [Pricing under rough volatility. Quant. Finance, 2016, 16(6), 887?904], is a promising rough volatility model in quantitative finance. It is a parsimonious model depending on only three parameters, and yet remarkably fits empirical implied volatility surfaces. In the absence of analytical European option pricing methods for the model, and due to the non-Markovian nature of the fractional driver, the prevalent option is to use the Monte Carlo (MC) simulation for pricing. Despite recent advances in the MC method in this context, pricing under the rBergomi model is still a time-consuming task. To overcome this issue, we have designed a novel, hierarchical approach, based on: (i) adaptive sparse grids quadrature (ASGQ), and (ii) quasi-Monte Carlo (QMC). Both techniques are coupled with a Brownian bridge construction and a Richardson extrapolation on the weak error. By uncovering the available regularity, our hierarchical methods demonstrate substantial computational gains with respect to the standard MC method. They reach a sufficiently small relative error tolerance in the price estimates across different parameter constellations, even for very small values of the Hurst parameter. Our work opens a new research direction in this field, i.e. to investigate the performance of methods other than Monte Carlo for pricing and calibrating under the rBergomi model. -
P. Pigato, Extreme at-the-money skew in a local volatility model, Finance and Stochastics, 23 (2019), pp. 827--859, DOI 10.1007/s00780-019-00406-2 .
-
A. Lejay, P. Pigato, A threshold model for local volatility: Evidence of leverage and mean reversion effects on historical data, International Journal of Theoretical and Applied Finance, 22 (2019), pp. 1950017/1--1950017/24, DOI 10.1142/S0219024919500171 .
-
CH. Bayer, P. Friz, A. Gulisashvili, B. Horvath, B. Stemper, Short-time near-the-money skew in rough fractional volatility models, Quantitative Finance, 19 (2019), pp. 779--798, DOI 10.1080/14697688.2018.1529420 .
Abstract
We consider rough stochastic volatility models where the driving noise of volatility has fractional scaling, in the "rough" regime of Hurst parameter H < ½. This regime recently attracted a lot of attention both from the statistical and option pricing point of view. With focus on the latter, we sharpen the large deviation results of Forde-Zhang (2017) in a way that allows us to zoom-in around the money while maintaining full analytical tractability. More precisely, this amounts to proving higher order moderate deviation estimates, only recently introduced in the option pricing context. This in turn allows us to push the applicability range of known at-the-money skew approximation formulae from CLT type log-moneyness deviations of order t1/2 (recent works of Alòs, León & Vives and Fukasawa) to the wider moderate deviations regime. -
P. Pigato, Tube estimates for diffusion processes under a weak Hörmander condition, Annales de l'Institut Henri Poincare. Probabilites et Statistiques, 54 (2018), pp. 299--342, DOI 10.1214/16-AIHP805 .
Abstract
We consider a diffusion process under a local weak Hörmander condition on the coefficients. We find Gaussian estimates for the density in short time and exponential lower and upper bounds for the probability that the diffusion remains in a small tube around a deterministic trajectory (skeleton path). These bounds depend explicitly on the radius of the tube and on the energy of the skeleton path. We use a norm which reflects the non-isotropic structure of the problem, meaning that the diffusion propagates in R2 with different speeds in the directions ? and [?,b]. We establish a connection between this norm and the standard control distance. -
CH. Bayer, P. Friz, A. Gulisashvili, B. Horvath, B. Stemper, Short-time near-the-money skew in rough fractional volatility models, Quantitative Finance, 19 (2019), pp. 779--798 (published online on 13.11.2018), DOI 10.1080/14697688.2018.1529420 .
Abstract
We consider rough stochastic volatility models where the driving noise of volatility has fractional scaling, in the "rough" regime of Hurst parameter H < ½. This regime recently attracted a lot of attention both from the statistical and option pricing point of view. With focus on the latter, we sharpen the large deviation results of Forde-Zhang (2017) in a way that allows us to zoom-in around the money while maintaining full analytical tractability. More precisely, this amounts to proving higher order moderate deviation estimates, only recently introduced in the option pricing context. This in turn allows us to push the applicability range of known at-the-money skew approximation formulae from CLT type log-moneyness deviations of order t1/2 (recent works of Alòs, León & Vives and Fukasawa) to the wider moderate deviations regime. -
CH. Bayer, H. Mai, J.G.M. Schoenmakers, Forward-reverse expectation-maximization algorithm for Markov chains: Convergence and numerical analysis, Advances in Applied Probability, 2 (2018), pp. 621--644, DOI 10.1017/apr.2018.27 .
Abstract
We develop a forward-reverse expectation-maximization (FREM) algorithm for estimating parameters of a discrete-time Markov chain evolving through a certain measurable state-space. For the construction of the FREM method, we develop forward-reverse representations for Markov chains conditioned on a certain terminal state. We prove almost sure convergence of our algorithm for a Markov chain model with curved exponential family structure. On the numerical side, we carry out a complexity analysis of the forward-reverse algorithm by deriving its expected cost. Two application examples are discussed. -
CH. Bayer, U. Horst, J. Qiu, A functional limit theorem for limit order books with state dependent price dynamics, The Annals of Applied Probability, 27 (2017), pp. 2753-2806.
Abstract
We consider a stochastic model for the dynamics of the two-sided limit order book (LOB). For the joint dynamics of best bid and ask prices and the standing buy and sell volume densities, we derive a functional limit theorem, which states that our LOB model converges to a continuous-time limit when the order arrival rates tend to infinity, the impact of an individual order arrival on the book as well as the tick size tend to zero. The limits of the standing buy and sell volume densities are described by two linear stochastic partial differential equations, which are coupled with a two-dimensional reflected Brownian motion that is the limit of the best bid and ask price processes. -
D. Belomestny, J.G.M. Schoenmakers, Statistical inference for time-changed Lévy processes via Mellin transform approach, Stochastic Processes and their Applications, 126 (2016), pp. 2092--2122.
-
G.N. Milstein, J.G.M. Schoenmakers, Uniform approximation of the CIR process via exact simulation at random times, Advances in Applied Probability, 48 (2016), pp. 1095--1116.
Abstract
In this paper we uniformly approximate the trajectories of the Cox-Ingersoll-Ross (CIR) process. At a sequence of random times the approximate trajectories will be even exact. In between, the approximation will be uniformly close to the exact trajectory. From a conceptual point of view the proposed method gives a better quality of approximation in a path-wise sense than standard, or even exact simulation of the CIR dynamics at some deterministic time grid. -
CH. Bayer, P. Friz, J. Gatheral, Pricing under rough volatility, Quantitative Finance, 16 (2016), pp. 887--904.
Abstract
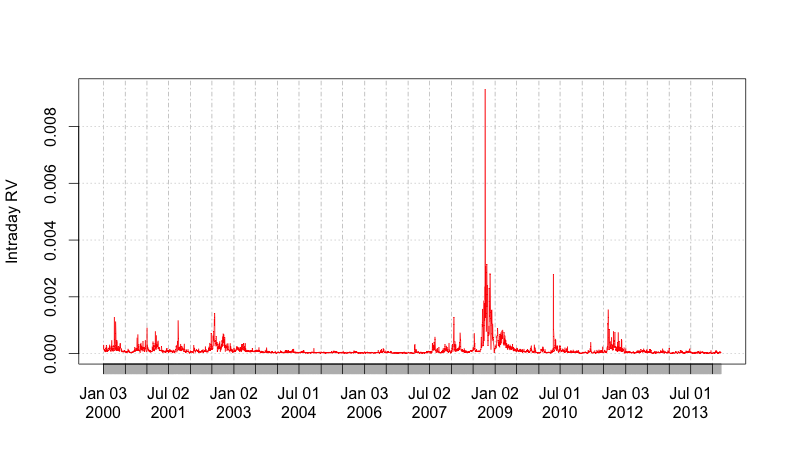
From an analysis of the time series of volatility using recent high frequency data, Gatheral, Jaisson and Rosenbaum [SSRN 2509457, 2014] previously showed that log-volatility behaves essentially as a fractional Brownian motion with Hurst exponent H of order 0.1, at any reasonable time scale. The resulting Rough Fractional Stochastic Volatility (RFSV) model is remarkably consistent with financial time series data. We now show how the RFSV model can be used to price claims on both the underlying and integrated volatility. We analyze in detail a simple case of this model, the rBergomi model. In particular, we find that the rBergomi model fits the SPX volatility markedly better than conventional Markovian stochastic volatility models, and with fewer parameters. Finally, we show that actual SPX variance swap curves seem to be consistent with model forecasts, with particular dramatic examples from the weekend of the collapse of Lehman Brothers and the Flash Crash. -
Z. Grbac, A. Papapantoleon, J.G.M. Schoenmakers, D. Skovmand, Affine LIBOR models with multiple curves: Theory, examples and calibration, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 6 (2015), pp. 984--1025.
Abstract
We introduce a multiple curve LIBOR framework that combines tractable dynamics and semi-analytic pricing formulas with positive interest rates and basis spreads. The dynamics of OIS and LIBOR rates are specified following the methodology of the affine LIBOR models and are driven by the wide and flexible class of affine processes. The affine property is preserved under forward measures, which allows to derive Fourier pricing formulas for caps, swaptions and basis swaptions. A model specification with dependent LIBOR rates is developed, that allows for an efficient and accurate calibration to a system of caplet prices. -
G.N. Milstein, J.G.M. Schoenmakers, Uniform approximation of the Cox--Ingersoll--Ross process, Advances in Applied Probability, 47 (2015), pp. 1132--1156.
Abstract
The Doss-Sussmann (DS) approach is used for simulating the Cox-Ingersoll-Ross (CIR) process. The DS formalism allows for expressing trajectories of the CIR process by solutions of some ordinary differential equation (ODE) that depend on realizations of the Wiener process involved. Via simulating the first-passage times of the increments of the Wiener process to the boundary of an interval and solving an ODE, we approximately construct the trajectories of the CIR process. From a conceptual point of view the proposed method may be considered as an exact simulation approach. -
J.D. Deuschel, P. Friz, A. Jacquier, S. Violante , Marginal density expansions for diffusions and stochastic volatility: Part I, Communications on Pure and Applied Mathematics, 67 (2014), pp. 40--82.
-
J.D. Deuschel, P. Friz, A. Jacquier, S. Violante , Marginal density expansions for diffusions and stochastic volatility: Part II, Communications on Pure and Applied Mathematics, 67 (2014), pp. 321--350.
-
G. Milshteyn, V. Spokoiny, Construction of mean-self-financing strategies for European options under regime-switching, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 5 (2014), pp. 532--556.
Abstract
The paper focuses on the problem of pricing and hedging a European contingent claim for an incomplete market model, in which evolution of price processes for a saving account and stocks depends on an observable Markov chain. The pricing function is evaluated using the martingale approach. The equivalent martingale measure is introduced in a way that the Markov chain remains the historical one. Due to the Markovian structure of the considered model, the pricing function satisfies the Cauchy problem for a system of linear parabolic partial differential equations. It is shown that any European contingent claim is attainable using a generalized replicating strategy which is self-financing in mean. For such a strategy, apart from the initial endowment and trading, some additional funds are required both step-wise at the jump moments of the Markov chain and continuously between the jump moments. The connection of the considered pricing and hedging problems with partial differential equations is very useful for computations. -
CH. Bayer, B. Veliyev, Utility maximization in a binomial model with transaction costs: A duality approach based on the shadow price process, International Journal of Theoretical and Applied Finance, 17 (2014), pp. 1450022/1--1450022/27.
-
CH. Bayer, J. Gatheral, M. Karlsmark, Fast Ninomiya--Victoir calibration of the double-mean-reverting model, Quantitative Finance, 13 (2014), pp. 1813--1829.
-
CH. Bayer, P. Laurence, Asymptotics beats Monte Carlo: The case of correlated local vol baskets, Communications on Pure and Applied Mathematics, 67 (2014), pp. 1618--1657.
-
CH. Bayer, J.G.M. Schoenmakers, Simulation of forward-reverse stochastic representations for conditional diffusions, The Annals of Applied Probability, 24 (2014), pp. 1994--2032.
Abstract
In this paper we derive stochastic representations for the finite dimensional distributions of a multidimensional diffusion on a fixed time interval, conditioned on the terminal state. The conditioning can be with respect to a fixed point or more generally with respect to some subset. The representations rely on a reverse process connected with the given (forward) diffusion as introduced in Milstein et al. [Bernoulli, 10(2):281-312, 2004] in the context of a forward-reverse transition density estimator. The corresponding Monte Carlo estimators have essentially root-N accuracy, hence they do not suffer from the curse of dimensionality. We provide a detailed convergence analysis and give a numerical example involving the realized variance in a stochastic volatility asset model conditioned on a fixed terminal value of the asset. -
M. Ladkau, J.G.M. Schoenmakers, J. Zhang, Libor model with expiry-wise stochastic volatility and displacement, International Journal of Portfolio Analysis and Management, 1 (2013), pp. 224--249.
Abstract
We develop a multi-factor stochastic volatility Libor model with displacement, where each individual forward Libor is driven by its own square-root stochastic volatility process. The main advantage of this approach is that, maturity-wise, each square-root process can be calibrated to the corresponding cap(let)vola-strike panel at the market. However, since even after freezing the Libors in the drift of this model, the Libor dynamics are not affine, new affine approximations have to be developed in order to obtain Fourier based (approximate) pricing procedures for caps and swaptions. As a result, we end up with a Libor modeling package that allows for efficient calibration to a complete system of cap/swaption market quotes that performs well even in crises times, where structural breaks in vola-strike-maturity panels are typically observed. -
S. De Marco, P. Friz, S. Gerhold, Don't stay local -- Extrapolation analytics for Dupire's local volatility, Risk Magazine, 29 Jan (2013), pp. 82--87.
-
CH. Bayer, P. Friz, R.L. Loeffen, Semi-closed form cubature and applications to financial diffusion models, Quantitative Finance, 13 (2013), pp. 769--782.
-
A. Mahayni, J.G.M. Schoenmakers, Minimum return guarantees with funds switching rights --- An optimal stopping problem, Journal of Economic Dynamics & Control, 35 (2012), pp. 1880--1897.
Abstract
Recently, there is a growing trend to offer guarantee products where the investor is allowed to shift her account/investment value between multiple funds. The switching right is granted a finite number per year, i.e. it is American style with multiple exercise possibilities. In consequence, the pricing and the risk management is based on the switching strategy which maximizes the value of the guarantee put option. We analyze the optimal stopping problem in the case of one switching right within different model classes and compare the exact price with the lower price bound implied by the optimal deterministic switching time. We show that, within the class of log-price processes with independent increments, the stopping problem is solved by a deterministic stopping time if (and only if) the price process is in addition continuous. Thus, in a sense, the Black & Scholes model is the only (meaningful) pricing model where the lower price bound gives the exact price. It turns out that even moderate deviations from the Black & Scholes model assumptions give a lower price bound which is really below the exact price. This is illustrated by means of a stylized stochastic volatility model setup. -
A. Papapantoleon, J.G.M. Schoenmakers, D. Skovmand, Efficient and accurate log-Lévy approximations to Lévy driven LIBOR models, Journal of Computational Finance, 15 (2012), pp. 3--44.
Abstract
The LIBOR market model is very popular for pricing interest rate derivatives, but is known to have several pitfalls. In addition, if the model is driven by a jump process, then the complexity of the drift term is growing exponentially fast (as a function of the tenor length). In this work, we consider a Lévy-driven LIBOR model and aim at developing accurate and efficient log-Lévy approximations for the dynamics of the rates. The approximations are based on truncation of the drift term and Picard approximation of suitable processes. Numerical experiments for FRAs, caps and swaptions show that the approximations perform very well. In addition, we also consider the log-Lévy approximation of annuities, which offers good approximations for high volatility regimes. -
M. Beiglboeck, P. Friz, S. Sturm, Is the minimum value of an option on variance generated by local volatility?, SIAM Journal on Financial Mathematics, ISSN 1945-497X, 2 (2011), pp. 213--220.
-
P. Friz, S. Gerhold, A. Gulisashvili, S. Sturm, On refined volatility smile expansion in the Heston model, Quantitative Finance, 11 (2011), pp. 1151--1164.
-
P. Imkeller, A. Réveillac, J. Zhang, Solvability and numerical simulation of BSDEs related to BSPDEs with applications to utility maximization, International Journal of Theoretical and Applied Finance, 14 (2011), pp. 635--667.
-
D. Belomestny, J.G.M. Schoenmakers, A jump-diffusion Libor model and its robust calibration, Quantitative Finance, 11 (2011), pp. 529--546.
-
V. Krätschmer, H. Zähle, Sensitivity of risk measures with respect to the normal approximation of total claim distributions, Insurance: Mathematics & Economics, 49 (2011), pp. 335--344.
Abstract
A simple and commonly used method to approximate the total claim distribution of a (possible weakly dependent) insurance collective is the normal approximation. In this article, we investigate the error made when the normal approximation is plugged in a fairly general distribution-invariant risk measure. We focus on the rate of the convergence of the error relative to the number of clients, we specify the relative error's asymptotic distribution, and we illustrate our results by means of a numerical example. Regarding the risk measure, we take into account distortion risk measures as well as distribution-invariant coherent risk measures. -
Y. Chen, W. Härdle, V. Spokoiny, GHICA --- Risk analysis with GH distributions and independent components, Journal of Empirical Finance, 17 (2010), pp. 255--269.
-
D. Belomestny, A. Kolodko, J.G.M. Schoenmakers, Pricing CMS spreads in the Libor market model, International Journal of Theoretical and Applied Finance, 13 (2010), pp. 45--62.
Abstract
We present two approximation methods for pricing of CMS spread options in Libor market models. Both approaches are based on approximating the underlying swap rates with lognormal processes under suitable measures. The first method is derived straightforwardly from the Libor market model. The second one uses a convexity adjustment technique under a linear swap model assumption. A numerical study demonstrates that both methods provide satisfactory approximations of spread option prices and can be used for calibration of a Libor market model to the CMS spread option market. -
R.L. Loeffen, J.-F. Renaud, De Finetti's optimal dividends problem with an affine penalty function at ruin, Insurance: Mathematics & Economics, 46 (2010), pp. 98--108.
-
A. Weiss, Escaping the Brownian stalkers, Electronic Journal of Probability, 14 (2009), pp. 139-160.
Abstract
We propose a simple model for the behaviour of long-time investors on stock markets, consisting of three particles, which represent the current price of the stock, and the opinion of the buyers, or sellers resp., about the right trading price. As time evolves both groups of traders update their opinions with respect to the current price. The update speed is controled by a parameter $gamma$, the price process is described by a geometric Brownian motion. The stability of the market is governed by the difference of the buyers' opinion and the sellers' opinion. We prove that the distance -
P. Friz, S. Benaim, Regular variation and smile asymptotics, Mathematical Finance. An International Journal of Mathematics, Statistics and Financial Economics, 19 (2009), pp. 1--12.
-
E. Giacomini, W. Härdle, V. Krätschmer, Dynamic semiparametric factor models in risk neutral density estimation, AStA. Advances in Statistical Analysis. A Journal of the German Statistical Society, 93 (2009), pp. 387--402.
-
D. Belomestny, J. Kampen, J.G.M. Schoenmakers, Holomorphic transforms with application to affine processes, Journal of Functional Analysis, 257 (2009), pp. 1222--1250.
Abstract
In a rather general setting of Itô?Lévy processes we study a class of transforms (Fourier for example) of the state variable of a process which are holomorphic in some disc around time zero in the complex plane. We show that such transforms are related to a system of analytic vectors for the generator of the process, and we state conditions which allow for holomorphic extension of these transforms into a strip which contains the positive real axis. Based on these extensions we develop a functional series expansion of these transforms in terms of the constituents of the generator. As application, we show that for multi-dimensional affine Itô?Lévy processes with state dependent jump part the Fourier transform is holomorphic in a time strip under some stationarity conditions, and give log-affine series representations for the transform -
D. Belomestny, S. Mathew, J.G.M. Schoenmakers, Multiple stochastic volatility extension of the Libor market model and its implementation, Monte Carlo Methods and Applications, 15 (2009), pp. 285-310.
Abstract
In this paper we propose a Libor model with a high-dimensional specially structured system of driving CIR volatility processes. A stable calibration procedure which takes into account a given local correlation structure is presented. The calibration algorithm is FFT based, so fast and easy to implement. -
D. Belomestny, G.N. Milstein, V. Spokoiny, Regression methods in pricing American and Bermudan options using consumption processes, Quantitative Finance, 9 (2009), pp. 315--327.
Abstract
Here we develop methods for efficient pricing multidimensional discrete-time American and Bermudan options by using regression based algorithms together with a new approach towards constructing upper bounds for the price of the option. Applying sample space with payoffs at the optimal stopping times, we propose sequential estimates for continuation values, values of the consumption process, and stopping times on the sample paths. The approach admits constructing both low and upper bounds for the price by Monte Carlo simulations. The methods are illustrated by pricing Bermudan swaptions and snowballs in the Libor market model. -
V. Krätschmer, Compactness in spaces of inner regular measures and a general Portmanteau lemma, Journal of Mathematical Analysis and Applications, 351 (2009), pp. 792--803.
-
R.L. Loeffen, An optimal dividends problem with transaction costs for spectrally negative Lévy processes, Insurance: Mathematics & Economics, 45 (2009), pp. 41--48.
-
J. Kampen, A. Kolodko, J.G.M. Schoenmakers, Monte Carlo Greeks for financial products via approximative transition densities, SIAM Journal on Scientific Computing, 31 (2008), pp. 1--22.
-
R. Krämer, P. Mathé, Modulus of continuity of Nemytskiĭ operators with application to a problem of option pricing, Journal of Inverse and Ill-Posed Problems, 16 (2008), pp. 435--461.
-
Y. Chen, W. Härdle, V. Spokoiny, Portfolio value at risk based on independent components analysis, Journal of Computational and Applied Mathematics, 205 (2007), pp. 594--607.
Abstract
Risk management technology applied to high-dimensional portfolios needs simple and fast methods for calculation of value at risk (VaR). The multivariate normal framework provides a simple off-the-shelf methodology but lacks the heavy-tailed distributional properties that are observed in data. A principle component-based method (tied closely to the elliptical structure of the distribution) is therefore expected to be unsatisfactory. Here, we propose and analyze a technology that is based on independent component analysis (ICA). We study the proposed ICVaR methodology in an extensive simulation study and apply it to a high-dimensional portfolio situation. Our analysis yields very accurate VaRs. -
CH. Fries, J. Kampen, Proxy simulation schemes for generic robust Monte Carlo sensitivities, process-oriented importance sampling and high-accuracy drift approximation, Journal of Computational Finance, 10 (2007), pp. 97--128.
Abstract
We consider a generic framework for generating likelihood ratio weighted Monte Carlo simulation paths, where we use one simulation scheme (proxy scheme) to generate realizations and then reinterpret them as realizations of another scheme (target scheme) by adjusting measure (via likelihood ratio) to match the distribution. This makes the approach independent of the product (the function f) and even of the model, it only depends on the numerical scheme. The approach is essentially a numerical version of the likelihood ratio method and Malliavin's Calculus reconsidered on the level of the discrete numerical simulation scheme. Since the numerical scheme represents a time discrete stochastic process sampled on a discrete probability space the essence of the method may be motivated without a deeper mathematical understanding of the time continuous theory (e.g. Malliavin's Calculus). The framework is completely generic and may be used for high accuracy drift approximations, process oriented importance sampling and the robust calculation of partial derivatives of expectations w.r.t. model parameters (i.e. sensitivities, aka. Greeks) by applying finite differences by reevaluating the expectation with a model with shifted parameters. We present numerical results using a Monte-Carlo simulation of the LIBOR Market Model for benchmarking. -
O. Reiss, J.G.M. Schoenmakers, M. Schweizer, From structural assumptions to a link between assets and interest rates, Journal of Economic Dynamics & Control, 31 (2007), pp. 593--612.
Abstract
We derive a link between assets and interest rates in a standard multi-asset diffusion economy from two structural assumptions ? one on the volatility and one on the short rate function. Our main result is economically intuitive and testable from data since it only involves empirically observable quantities. A preliminary study illustrates how this could be done. -
H. Haaf, O. Reiss, J.G.M. Schoenmakers, Numerically stable computation of CreditRisk+, Phys. Rev. E (3), 6 (2004), pp. 1--10.
Abstract
The CreditRisk+ model launched by Credit Suisse First Boston in 1997 is widely used by practitioners in the banking sector as a simple means for the quantification of credit risk, primarily of the loan book. We present an alternative numerical recursion scheme for CreditRisk+, equivalent to an algorithm recently proposed by Giese, that is based on well-known expansions of the logarithm and the exponential of a power series. We show that it is advantageous for the Panjer recursion advocated in the original CreditRisk+ document, in that it is numerically stable. The crucial stability arguments are explained in detail. We explain how to apply the suggested recursion scheme to incorporate stochastic exposures into the CreditRisk+ model as introduced by Tasche (2004). Finally, the computational complexity of the resulting algorithm is stated and compared with other methods for computing the CreditRisk+ loss distribution. -
J.G.M. Schoenmakers, B. Coffey, Systematic generation of parametric correlation structures for the LIBOR market model, International Journal of Theoretical and Applied Finance, 6 (2003), pp. 507-519.
Abstract
We present a conceptual approach of deriving parsimonious correlation structures suitable for implementation in the LIBOR market model. By imposing additional constraints on a known ratio correlation structure, motivated by economically sensible assumptions concerning forward LIBOR correlations, we yield a semi-parametric framework of non-degenerate correlation structures with realistic properties. Within this framework we derive systematically low parametric structures with, in principal, any desired number of parameters. As illustrated, such structures may be used for smoothing a matrix of historically estimated LIBOR return correlations. In combination with a suitably parametrized deterministic LIBOR volatility norm we so obtain a parsimonious multi-factor market model which allows for joint calibration to caps and swaptions. See Schoenmakers [2002] for a stable full implied calibration procedure based on the correlation structures developed in this paper. -
O. Kurbanmuradov, K. Sabelfeld, J.G.M. Schoenmakers, Lognormal approximations to LIBOR market models, Journal of Computational Finance, 6 (2002), pp. 69--100.
Abstract
We study several lognormal approximations for LIBOR market models, where special attention is paid to their simulation by direct methods and lognormal random fields. In contrast to conventional numerical solution of SDE's this approach simulates the solution directly at a desired point in time and therefore may be more efficient. As such the proposed approximations provide valuable alternatives to the Euler method, in particular for long dated instruments. We carry out a path-wise comparison of the different lognormal approximations with the 'exact' SDE solution obtained by the Euler scheme using sufficiently small time steps. Also we test approximations obtained via numerical solution of the SDE by the Euler method, using larger time steps. It turns out that for typical volatilities observed in practice, improved versions of the lognormal approximation proposed by Brace, Gatarek and Musiela, citeBrace, appear to have excellent path-wise accuracy. We found out that this accuracy can also be achieved by Euler stepping the SDE using larger time steps, however, from a comparative cost analysis it follows that, particularly for long maturity options, the latter method is more time consuming than the lognormal approximation. We conclude with applications to some example LIBOR derivatives. -
G.N. Milstein, J.G.M. Schoenmakers, Numerical construction of hedging strategies against multi-asset European claims, Stochastics and Stochastics Reports, 73 (2002), pp. 125--157.
Abstract
For evaluating a hedging strategy we have to know at every moment the solution of the Cauchy problem for a corresponding parabolic equation (the value of the hedging portfolio) and its derivatives (the deltas). We suggest to find these quantities by Monte Carlo simulation of the corresponding system of stochastic differential equations using weak solution schemes. It turns out that with one and the same control function a variance reduction can be achieved simultaneously for the claim value as well as for the deltas. As illustrations we consider a Markovian multi-asset model with an instantaneously riskless saving bond and also some applications to the LIBOR rate model of Brace, Gatarek, Musiela and Jamshidian.
 Contributions to Collected Editions
Contributions to Collected Editions
-
CH. Bayer, P. Laurence, Small-time asymptotics for the at-the-money implied volatility in a multi-dimensional local volatility model, in: Large Deviations and Asymptotic Methods in Finance, P. Friz, J. Gatheral, A. Gulisashvili, A. Jaquier, J. Teichmann, eds., 110 of Springer Proceedings in Mathematics & Statistics, Springer, Berlin et al., 2015, pp. 213--237.
-
J.G.M. Schoenmakers, SHOWCASE 17 -- Expiry-wise Heston LIBOR model, in: MATHEON -- Mathematics for Key Technologies, M. Grötschel, D. Hömberg, J. Sprekels, V. Mehrmann ET AL., eds., 1 of EMS Series in Industrial and Applied Mathematics, European Mathematical Society Publishing House, Zurich, 2014, pp. 314--315.
-
H.-G. Bartel, H.-J. Mucha, J. Dolata, Geochemical and statistical investigation of Roman stamped tiles of the Legio XXI Rapax, in: Classification as a Tool for Research. 11th IFCS Biennial Conference and 33rd Annual Conference of the Gesellschaft für Klassifikation e. V., Dresden, March 13--18, 2009, H. Locarek-Junge, C. Weihs, eds., Studies in Classification, Data Analysis, and Knowledge Organization, Springer, Berlin/Heidelberg, 2010, pp. 427--434.
-
P. Friz, M. Keller-Ressel, Moment explosions in financial models, in: Encyclopedia of Quantitative Finance, R. Cont, ed., Wiley, Chichester, 2010, pp. 1247--1253.
-
P. Friz, Implied volatility: Large strike asymptotics, in: Encyclopedia of Quantitative Finance, R. Cont, ed., Wiley, Chichester, 2010, pp. 909--913.
-
M. Elagin, V. Spokoiny, Locally time homogeneous time series modelling, in: Applied Quantitative Finance (2nd edition), W. Härdle, N. Hautsch, L. Overbeck, eds., Springer, Berlin, 2008, pp. 345--362.
-
J. Kampen, On optimal strategies of multivariate passport options, in: Progress in Industrial Mathematics at ECMI 2006, L.L. Bonilla, M. Moscoso, G. Platero, J.M. Vega, eds., 12 of Mathematics in Industry, Springer, Berlin, Heidelberg, 2008, pp. 666--670.
-
C. Croitoru, Ch. Fries, W. Jäger, J. Kampen, D.-J. Nonnenmacher, On the dynamics of the forward interest rate curve and the evaluation of interest rate derivatives and their sensitivities, in: Mathematics --- Key Technology for the Future, W. Jäger, H.-J. Krebs, eds., Springer, Heidelberg, 2008, pp. 343--357.
-
H. Haaf, O. Reiss, J.G.M. Schoenmakers, Numerically stable computation of Credit Risk+, in: CreditRisk+ in the Banking Industry, M. Gundlach, F. Lehrbass, eds., XII, Springer, Berlin Heidelberg, 2004, pp. 67-76.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
CH. Bayer, L. Pelizzari, J.G.M. Schoenmakers, Primal and dual optimal stopping with signatures, Preprint no. 3068, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3068 .
Abstract, PDF (458 kByte)
We propose two signature-based methods to solve the optimal stopping problem - that is, to price American options - in non-Markovian frameworks. Both methods rely on a global approximation result for Lp-functionals on rough path-spaces, using linear functionals of robust, rough path signatures. In the primal formulation, we present a non-Markovian generalization of the fa- mous Longstaff--Schwartz algorithm, using linear functionals of the signature as regression basis. For the dual formulation, we parametrize the space of square-integrable martingales using linear functionals of the signature, and apply a sample average approximation. We prove convergence for both methods and present first numerical examples in non-Markovian and non-semimartingale regimes. -
CH. Bayer, D. Belomestny, O. Butkovsky, J.G.M. Schoenmakers, RKHS regularization of singular local stochastic volatility McKean--Vlasov models, Preprint no. 2921, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2921 .
Abstract, PDF (504 kByte)
Motivated by the challenges related to the calibration of financial models, we consider the problem of solving numerically a singular McKean-Vlasov equation, which represents a singular local stochastic volatility model. Whilst such models are quite popular among practitioners, unfortunately, its well-posedness has not been fully understood yet and, in general, is possibly not guaranteed at all. We develop a novel regularization approach based on the reproducing kernel Hilbert space (RKHS) technique and show that the regularized model is well-posed. Furthermore, we prove propagation of chaos. We demonstrate numerically that a thus regularized model is able to perfectly replicate option prices due to typical local volatility models. Our results are also applicable to more general McKean--Vlasov equations.
 Talks, Poster
Talks, Poster
-
O. Butkovsky, Strong rate of convergence of the Euler scheme for SDEs with irregular drift driven by Levy noise, 14th Conference on Monte Carlo Methods and Applications, June 26 - 30, 2023, Sorbonne University, Paris, France, June 29, 2023.
-
S. Breneis, An error representation formula for the log-ode method, 15th Berlin-Oxford Young Researcher's Meeting on Applied Stochastic Analysis, May 12 - 14, 2022, WIAS & TU Berlin, May 14, 2022.
-
S. Breneis, An error representation formula for the log-ode method, 16th Oxford-Berlin Young Researcher's Meeting on Applied Stochastic Analysis, December 8 - 10, 2022, University of Oxford, UK, December 9, 2022.
-
S. Breneis, Markovian approximations for rough volatility models, Seminar Stochastic Numerics Research Group, King Abdullah University of Science and Technology, Thuval, Saudi Arabia, January 26, 2022.
-
S. Breneis, Markovian approximations of rough volatility models, Mathematics of Random Systems Summer School 2022, September 25 - 30, 2022, University of Oxford, St Hugh's College, UK, September 29, 2022.
-
CH. Bayer, Efficient Markovian approximation of rough stochastic volatility models (online talk), Aarhus/SMU Volatility Workshop (Online Event), Aarhus University, Department of Economics and Business, Denmark, May 31, 2022.
-
CH. Bayer, Efficient Markovian approximation to rough volatility models, Rough Volatility Meeting, Imperial College London, UK, March 16, 2022.
-
CH. Bayer, Machine learning techniques in computational finance, Stochastic Numerics and Statistical Learning: Theory and Applications Workshop, May 15 - 28, 2022, King Abdullah University, Computer, Electrical and Mathematical Sciences and Engineering Division, Thuwal, Saudi Arabia, May 22, 2022.
-
CH. Bayer, Simulating rough volatility models (online talk), MathFinance 2022 Conference (Online Event), March 21 - 22, 2022, March 22, 2022.
-
S. Breneis, Markovian approximations of stochastic Volterra equations with the fractional kernel, 2021 Summer School of Berlin-Oxford IRTG Stochastic Analysis in Interaction (Hybrid Event), September 20 - 24, 2021, Technische Universität Berlin, Institut für Mathematik, September 24, 2021.
-
S. Breneis, Markovian approximations of stochastic volatility models (online talk), 16. DoktorandInnentreffen der Stochastik (Online Event), Ludwig-Maximilians-Universität München, Fakultät für Mathematik, Informatik und Statistik, July 30, 2021.
-
S. Breneis, On variation functions and their moduli of continuity (online talk), Methods of Nonlinear Analysis in Differential and Integral Equations (Online Event), May 15 - 16, 2021, Rzeszów University of Technology, Department of Nonlinear Analysis, Poland, May 16, 2021.
-
CH. Bayer, A pricing BSPDE for rough volatility (online talk), MATH4UQ Seminar (Online Event), Rheinisch-Westfälische Technische Hochschule Aachen, Mathematics for Uncertainty Quantification, April 6, 2021.
-
P. Friz, Local volatility under rough volatility, QuantMinds International 2021, December 6 - 9, 2021, Barcelona, Spain, December 7, 2021.
-
P. Friz, New perspectives on rough paths, signatures and signature cumulants (online talk), DataSig Seminar Series (Online Event), University of Oxford, Mathematical Institute, UK, May 6, 2021.
-
CH. Bayer, A regularity structure for rough volatility, Vienna Seminar in Mathematical Finance and Probability, Technische Universität Wien, Research Unit of Financial and Actuarial Mathematics, Austria, January 10, 2019.
-
CH. Bayer, Calibration of rough volatility models by deep learning, Rough Workshop 2019, September 4 - 6, 2019, Technische Universität Wien, Financial and Actuarial Mathematics, Austria.
-
CH. Bayer, Deep calibration of rough volatility models, New Directions in Stochastic Analysis: Rough Paths, SPDEs and Related Topics, WIAS und TU Berlin, March 18, 2019.
-
CH. Bayer, Deep calibration of rough volatility models, SIAM Conference on Financial Mathematics & Engineering, June 4 - 7, 2019, Society for Industrial and Applied Mathematics, Toronto, Ontario, Canada, June 7, 2019.
-
CH. Bayer, Learning rough volatility, Algebraic and Analytic Perspectives in the Theory of Rough Paths and Signatures, November 14 - 15, 2019, University of Oslo, Department of Mathematics, Norway, November 14, 2019.
-
CH. Bayer, Numerics for rough volatility, Stochastic Processes and Related Topics, February 21 - 22, 2019, Kansai University, Senriyama Campus, Osaka, Japan, February 22, 2019.
-
CH. Bayer, Pricing American options by exercise rate optimization, Workshop on Financial Risks and Their Management, February 19 - 20, 2019, Ryukoku University, Wagenkan, Kyoto, Japan, February 19, 2019.
-
P. Pigato, Asymptotic analysis of rough volatility models, Probability Seminar, L'Università di Milano-Bicocca, Dipartimento di Matematica e Applicazioni, Italy, July 13, 2018.
-
P. Pigato, Asymptotic analysis of rough volatility models, Seminar of the Research Training Group 2131, Ruhr-Universität Bochum, June 25, 2018.
-
P. Pigato, Density and tube estimates for diffusion processes under Hormander-type conditions, Séminaire (de Calcul) Stochastique, Université de Strasbourg, Institut de Recherche Mathématique Avancée, France, November 23, 2018.
-
P. Pigato, Faits stilisés et modélisation de la volatilité, École Polytechnique, Université Paris-Saclay, Département de Mathématiques Appliquées, Palaiseau, France, April 20, 2018.
-
P. Pigato, Faits stilisés et modélisation de la volatilité, Seminaire, Institut de Science Financière et d'Assurances, Université Lyon 1, France, May 14, 2018.
-
P. Pigato, Precise asymptotics of rough stochastic volatility models, University of Trento, Department of Mathematics, November 16, 2018.
-
P. Pigato, Short dated option pricing under rough volatility, Berlin-Paris Young Researchers Workshop Stochastic Analysis with applications in Biology and Finance, May 2 - 4, 2018, Institut des Systèmes Complexes de Paris Ile-de-France (ISC-PIF), National Center for Scientific Research, Paris, France, May 4, 2018.
-
CH. Bayer, Short-time near-the-money skew in rough fractional volatility models, 9-th International Workshop on Applied Probability, June 18 - 21, 2018, Eörvös Loránd University (ELU), Budapest, Hungary, June 19, 2018.
-
CH. Bayer, Rough volatility models in finance, 19th International Congress of the ÖMG and Annual DMV Meeting, 6th Austrian Stochastics Days, September 11 - 15, 2017, Austrian Mathematical Society (ÖMG) and Deutsche Mathematiker-Vereinigung (DMV), Paris-Lodron University of Salzburg, Austria, September 13, 2017.
-
CH. Bayer, Rough volatility models in finance, AMCS Seminar, King Abdullah University of Science and Technology (KAUST), Computer, Electrical and Mathematical Sciences & Engineering Division, Thuwal, Saudi Arabia, October 25, 2017.
-
CH. Bayer, Smoothing the payoff for efficient computation of basket option prices, Workshop ``Mathematics of Quantitative Finance'', February 26 - March 4, 2017, Mathematisches Forschungsinstitut Oberwolfach, February 27, 2017.
-
CH. Bayer, Smoothing the payoff for efficient computation of basket options, Workshop on Recent Developments in Numerical Methods with Applications in Statistics and Finance, June 8 - 9, 2017, University of Mannheim, Graduate School of Economics and Social Sciences, June 9, 2017.
-
CH. Bayer, Smoothing the payoff for efficient computation of basket options, Conference on Mathematical Modelling in Finance 2017, August 30 - September 2, 2017, Imperial College London, UK, September 2, 2017.
-
J.G.M. Schoenmakers, Projective simulation and regression methods for Mckean--Vlasov SDE systems, Mathematisches Kolloquium, Universität Duisburg-Essen, Fakultät für Mathematik, November 29, 2017.
-
CH. Bayer, Pricing under rough volatility, Statistics for Differential Equations driven by Rough Paths, September 7 - 8, 2016, University of Warwick, Centre for Research in Statistical Methodology, Coventry, UK, September 7, 2016.
-
CH. Bayer, Pricing under rough volatility, Vienna Congress on Mathematical Finance -- VCMF 2016, September 12 - 14, 2016, Vienna University of Economics and Business, Austria, September 12, 2016.
-
CH. Bayer, Pricing under rough volatility, Czech, Slovenian, Austrian, Slovak and Catalan Mathematical Societies Joint Meeting 2016, September 20 - 23, 2016, Societat Catalana de Matemàtiques, Institut d'Estudis Catalans, Barcelona, Spain, September 20, 2016.
-
CH. Bayer, Short dated option prices under rough volatility, Rough Volatility Meeting, October 7 - 8, 2016, Imperial College London, Department of Mathmatics, UK, October 7, 2016.
-
J.G.M. Schoenmakers, Financial Mathematics, The 9th Summer School in Financial Mathematics 2016, February 18 - 20, 2016, African Institute for Mathematical Sciences South Africa (AIMS), Cape Town.
-
J.G.M. Schoenmakers, Uniform approximation methods for the C.I.R. process, Stochastic Seminar, Charles University, Prague, Czech Republic, April 6, 2016.
-
J.G.M. Schoenmakers, Uniform approximation of the Cox--Ingersoll--Ross process, Frontiers in Stochastic Modelling for Finance, February 2 - 6, 2016, Università degli Studi di Padova, Padua, Italy, February 5, 2016.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local vol baskets, Groupe de Travail: Finance Mathématique, Probabilités Numériques et Statistique des Processus, Université Paris Diderot, Laboratoire de Probabilités et Modèles Aléatoires, France, February 19, 2015.
-
CH. Bayer, Pricing under rough volatility, Berlin-Princeton-Singapore Workshop on Quantitative Finance, June 29 - July 1, 2015, National University of Singapore, Centre for Quantitative Finance, Singapore, June 29, 2015.
-
CH. Bayer, Pricing under rough volatility, 38th Conference on Stochastic Processes and their Applications, July 13 - 17, 2015, University of Oxford, Oxford-Man Institute of Quantitative Finance, UK, July 15, 2015.
-
CH. Bayer, Pricing under rough volatility, Finanzmathematik, University of Vienna, Faculty of Mathematics, Austria, November 26, 2015.
-
CH. Bayer, Rough volatility, 3rd Annual ERC Berlin-Oxford Young Researchers Meeting on Applied Stochastic Analysis, January 27 - 29, 2015, WIAS Berlin, January 29, 2015.
-
M. Ladkau, A new multi-factor stochastic volatility model with displacement, First Berlin-Singapore Workshop on Quantitative Finance and Financial Risk, May 21 - 24, 2014, WIAS-Berlin und Humboldt-Universität zu Berlin, May 22, 2014.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local vol baskets, International Workshop ``Advances in Optimization and Statistics'', May 15 - 16, 2014, Russian Academy of Sciences, Institute of Information Transmission Problems (Kharkevich Institute), Moscow, May 16, 2014.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local vol baskets, First Berlin-Singapore Workshop on Quantitative Finance and Financial Risk, May 21 - 24, 2014, WIAS-Berlin und Humboldt-Universität zu Berlin, May 21, 2014.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local vol baskets, Workshop on Stochastic and Quantitative Finance, November 28 - 29, 2014, Imperial College London, UK, November 29, 2014.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correleated local vol baskets, Stochastic Analysis Seminar Series, Oxford-Man Institute, UK, January 27, 2014.
-
J.G.M. Schoenmakers, Affine LIBOR models with multiple curves: Theory, examples and calibration, 11th German Probability and Statistics Days 2014, March 5 - 7, 2014, Universität Ulm, March 6, 2014.
-
M. Ladkau, A new multi-factor stochastic volatility model with displacement, PreMoLab Workshop on: Advances in predictive modeling and optimization, May 16 - 17, 2013, WIAS-Berlin, May 16, 2013.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local volatility baskets, Stochastik-Seminar, Universität Heidelberg, Institut für angewandte Mathematik, June 18, 2013.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local volatility baskets, Seminar Finanzmathematik, Universität Wien, Austria, November 28, 2013.
-
CH. Bayer, Asymptotics can beat Monte Carlo, 20th Annual Global Derivatives & Risk Management, April 16 - 18, 2013, The International Centre for Business Information (ICBI), Amsterdam, Netherlands, April 18, 2013.
-
J.G.M. Schoenmakers, Simulation of conditional diffusions via forward-reverse stochastic representations, DynStoch 2013, April 17 - 19, 2013, University of Copenhagen, Department of Mathematical Sciences, Denmark, April 19, 2013.
-
J.G.M. Schoenmakers, Simulation of conditional diffusions via forward-reverse stochastic representations, PreMoLab Workshop on: Advances in predictive modeling and optimization, May 16 - 17, 2013, WIAS-Berlin, May 16, 2013.
-
CH. Bayer, Asymptotics beats Monte Carlo: The case of correlated local vol baskets, Applied Mathematics and Computational Science Seminar, King Abdullah University of Science and Technology, Saudi Arabia, December 5, 2012.
-
CH. Bayer, Some applications of the Ninomiya--Victoir scheme in the context of financial engineering, Talks in Financial and Insurance Mathematics, Eidgenössische Technische Hochschule Zürich, Switzerland, April 26, 2012.
-
CH. Bayer, Some applications of the Ninomiya--Victoir scheme in the context of financial engineering, Stochastic Analysis Seminar Series, Oxford University, Oxford-Man Institute of Quantitative Finance, UK, May 21, 2012.
-
H. Mai, Drift estimation for jump diffusion, Haindorf Seminar 2012 (Klausurtagung des SFB 649), February 9 - 12, 2012, Humboldt-Universität zu Berlin, Wirtschaftswissenschaftliche Fakultät, Hejnice, Czech Republic, February 10, 2012.
-
H. Mai, Parametric and nonparametric estimation for stochastic volatility models with jumps, 10th German Probalility and Statistic Days 2012, March 6 - 9, 2012, Johannes Gutenberg Universität Mainz, March 7, 2012.
-
V. Krätschmer, Central limit theorems for law-invariant risk measures, Conference on ``Modeling and managing financial risks'', Université Paris VI, École Polytechnique, France, January 11, 2011.
-
V. Panov, Affine stochastic volatility models: asymptotic behavior of the characteristic function and estimation of the Blumenthal - Getoor index, Tagung des SFB 649 "Ökonomisches Risiko" in Motzen, June 30 - July 2, 2011, Humboldt-Universität zu Berlin, Wirtschaftswissenschaftliche Fakultät, July 1, 2011.
-
R.L. Loeffen, Two methods for pricing European options, Colloquia on Probability and Statistics 2011, University of Bern, Institute of Mathematical Statistics and Actuarial Science, Switzerland, May 5, 2011.
-
R.L. Loeffen, Applying spectral representations for CBI processes to finance, Stochastic Networks and Related Topics III, May 22 - 25, 2011, Mathematical Research and Conference Center in Bedlewo, Poland, May 24, 2011.
-
R.L. Loeffen, Option pricing in affine term structure models via spectral representations, Seminar in Mathematical Finance, Universität Wien, Fakultät für Mathematik, Austria, January 31, 2011.
-
J.G.M. Schoenmakers, New dual methods for single and multiple exercise option, Universität Ulm, Institut für Numerische Mathematik, May 27, 2011.
-
J.G.M. Schoenmakers, New dual methods for single and multiple exercise options, Workshop ``Quantitative Methods in Financial and Insurance Mathematics'', April 18 - 21, 2011, Lorentz Center, Leiden, Netherlands, April 21, 2011.
-
J.G.M. Schoenmakers , New dual methods for single and multiple exercise options, International Workshop on Numerical Algorithms in Computational Finance, July 20 - 22, 2011, Goethe Universität Frankfurt, Goethe Center for Scientific Computing, July 22, 2011.
-
V. Krätschmer, A uniform central limit theorem for distortions of empirical distributions with applications to nonparametric estimation of distribution-invariant risk measures, Leipziger Stochastik Tage, March 1 - 5, 2010, Universität Leipzig, Fakultät für Mathematik und Informatik, March 2, 2010.
-
V. Krätschmer, Error caused by normal approximation of the total claim distribution when plugged in risk measures, 4th International Conference Mathematical and Statistical Methods for Actuarial Sciences and Finance, April 7 - 9, 2010, Università degli Studi di Salerno, Dipartimento di Scienze Economiche e Statistiche, Ravello, Italy, April 8, 2010.
-
V. Krätschmer, Error caused by normal approximation of the total claim distribution when plugged in risk measures, DAGStat2010, March 23 - 26, 2010, Technische Universität Dortmund, Fakultät Statistik, March 23, 2010.
-
V. Krätschmer, Nichtparametrische Schätzung verteilungsinvarianter Risikomaße, Universität Bayreuth, Fachbereich Mathematik, July 27, 2010.
-
V. Krätschmer, Nichtparametrische Schätzung verteilungsinvarianter Risikomaße, Universität Mannheim, Institut für Mathematik und Informatik, May 4, 2010.
-
V. Krätschmer, Nichtparametrische Schätzung verteilungsinvarianter Risikomaße, Heinrich Heine Universität Düsseldorf, Institut für Mathematik, April 23, 2010.
-
V. Krätschmer, Nonparametric estimation of low invariant risk measures for time series, Statistische Woche Nürnberg 2010, September 14 - 17, 2010, Deutschen Statistischen Gesellschaft (DStatG), September 16, 2010.
-
P. Friz, Stochastic analysis and quantitative finance, Microsoft Research Cambridge, UK, January 5, 2010.
-
R.L. Loeffen, Absolute ruin in the insurance risk model of Ornstein--Uhlenbeck type, 24th European Conference on Operational Research (EURO XXIV LISBON), July 11 - 14, 2010, Universidade de Lisboa, Faculdade de Ciéncias, Portugal, July 14, 2010.
-
R.L. Loeffen, The Ornstein--Uhlenbeck type risk model: Absolute ruin and spectral representation, Talks in Actuarial Sciences, Université Libre de Bruxelles, Département de Mathématiques, Belgium, November 18, 2010.
-
P. Mathé, Conjugate gradient iteration for statistical inverse problems, Rencontres de Statistiques Mathématiques 10, December 13 - 17, 2010, Centre International de Rencontres Mathématiques (CIRM), Luminy, France, December 15, 2010.
-
J.G.M. Schoenmakers, Advanced Libor modeling, Postbank Bonn, February 25, 2010.
-
J.G.M. Schoenmakers, Holomorphic transforms with application to affine processes, 5th General Conference in Advanced Mathematical Methods in Finance, May 4 - 8, 2010, University of Ljubljana, Faculty of Mathematics and Physics, Slovenia, May 6, 2010.
-
J.G.M. Schoenmakers, On three innovations in financial modeling, Colloquium, University of Twente, Faculty of Electrical Engineering, Mathematics and Computer Science, Netherlands, August 24, 2010.
-
B. Metzger, The discrete Gross--Pitaevskii model and condensation in the single particle ground state, Berlin-Leipzig Seminar on Analysis and Probability Theory, November 27, 2009, Technische Universität Berlin, Institut für Mathematik, November 27, 2009.
-
V. Panov, Pricing Bermudan options via dimension reduction, Klausurtagung des SFB 649, June 4 - 6, 2009, Humboldt-Universität zu Berlin, Motzen, June 5, 2009.
-
V. Panov, Solving classification task using detection of non-Gaussian components, Haindorf Seminar 2009, February 12 - 15, 2009, Humboldt-Universität zu Berlin, CASE --- Center for Applied Statistics and Economics, Hejnice, Czech Republic, February 14, 2009.
-
D. Peschka, Dewetting of thin liquid films on viscoelastic substrates, European Coating Symposium, September 7 - 9, 2009, Karlsruhe, September 7, 2009.
-
P. Friz, From numerical aspects of stochastic financial models to the foundations of stochastic differential equations (and back), Annual Meeting of the Deutsche Mathematiker-Vereinigung and 17th Congress of the Österreichische Mathematische Gesellschaft, Section ``Financial and Actuarial Mathematics'', September 20 - 25, 2009, Technische Universität Graz, Austria, September 25, 2009.
-
P. Friz, Rough paths and the gap between deterministic and stochastic differential equations, Berlin Mathematical School, Friday Colloquium, December 18, 2009.
-
R. Loeffen, De Finetti's optimal dividends problem with an affine penalty function at ruin, Université Libre de Bruxelles, Département de Mathématiques, Belgium, November 19, 2009.
-
CH. Meyer, Finite element error analysis for state-constrained optimal control of the Stokes problem, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Section ``Optimization of Differential Equations'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
A. Mielke, BV solutions and parametrized solutions for rate-independent systems, 80th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2009), Session ``Applied Analysis'', February 9 - 13, 2009, Gdansk University of Technology, Poland, February 10, 2009.
-
J.G.M. Schoenmakers, Holomorphic transforms with application to affine processes, Workshop ``Computational Finance'', August 10 - 12, 2009, Kyoto University, Faculty of Sciences, Japan, August 10, 2009.
-
J.G.M. Schoenmakers, Statistical and numerical methods for evaluation for financial derivates and risk, Center Days 2009 (DFG Research Center scshape Matheon), March 30 - April 1, 2009, Technische Universität Berlin, March 31, 2009.
-
J. Kampen, Higher order WKB expansions of the fundamental solution and pricing of options, Credit Suisse, Zurich, Switzerland, March 28, 2008.
-
J. Kampen, Holomorphic transforms with application to affine feller processess in finance, 5th World Congress, Bachelier Finance Society, July 16 - 19, 2008, Royal Geographical Institute, London, UK, July 18, 2008.
-
J. Kampen, Monte carlo greeks for financial prods via approximate transition densities, 5th World Congress, Bachelier Finance Society, July 16 - 19, 2008, Royal Geographical Institute, London, UK, July 19, 2008.
-
A. Weiss, Limit order books and optimal portfolio liquidation, Summer School 2008 Pro$^*$Doc/IRTG Berlin-Zürich ``Stochastic Models of Complex Processes'', July 21 - 25, 2008, Disentis, Switzerland, July 22, 2008.
-
P. Mathé, On non-stability of some inverse problem in option pricing, Workshop on Inverse and Partial Information Problems: Methodology and Applications, October 27 - 31, 2008, Austrian Academy of Sciences, Johann Radon Institute for Computational and Applied Mathematics (RICAM), Linz, October 30, 2008.
-
J.G.M. Schoenmakers, Holomorphic transforms and affine processes, Technische Universität Braunschweig, May 20, 2008.
-
J.G.M. Schoenmakers, Holomorphic transforms with application to affine processes, 2nd Meeting in the winter semester 2008/2009 of the Research Seminar ``Stochastic Analysis and Stochastics of Financial Markets'', Technische Universität Berlin, November 6, 2008.
-
J. Kampen, Closed form analytic expansion formulas for characteristic functions of affine jump diffusion processes, Workshop on Numerics in Finance, November 5 - 6, 2007, Commerzbank AG, Frankfurt/Main, November 6, 2007.
-
J.G.M. Schoenmakers, Robust Libor modelling and calibration, International Multidisciplinary Workshop on Stochastic Modeling, June 25 - 29, 2007, Sevilla, Spain, June 29, 2007.
-
A. Weiss, Escaping the Brownian stalkers, BRG Workshop on Stochastic Models from Biology and Physics, October 9 - 10, 2006, Johann Wolfgang Goethe-Universität Frankfurt, October 10, 2006.
-
A. Weiss, Escaping the Brownian stalkers, 5th Prague Summer School 2006 "`Statistical Mathematical Mechanics"', September 10 - 23, 2006, Charles University, Center for Theoretical Study and Institute of Theoretical Computer Science, Prague, Czech Republic, September 20, 2006.
-
J.G.M. Schoenmakers, A jump-diffusion Libor model and its robust calibration, 4th World Congress of the Bachelier Finance Society, August 17 - 20, 2006, National Center of Sciences, Hitotsubashi University, ICS, Tokyo, Japan, August 20, 2006.
-
J.G.M. Schoenmakers, Interest rate modelling: Practical calibration and implementation techniques, June 15 - 16, 2006, Risk, London, UK.
-
J.G.M. Schoenmakers, Robust Libor modelling and pricing of derivative products, Delft University of Technology, Netherlands, June 9, 2005.
-
J.G.M. Schoenmakers, Interest rate modelling --- Practical calibration and implementation techniques, Incisive Media Events, Hong Kong, China, December 8, 2004.
-
J.G.M. Schoenmakers, Numerically stable computation of CreditRisk+, Karlsruher Stochastik-Tage 2004, March 23 - 26, 2004, Universität Karlsruhe, March 25, 2004.
-
J.G.M. Schoenmakers, Kreditrisiko Portfolio-Modelle, Kreditanstalt für Wiederaufbau, Frankfurt, July 18, 2003.
-
J.G.M. Schoenmakers, Robust calibration of LIBOR market models, Petit Dejeuner de la Finance, November 4 - 5, 2003, Paris, November 5, 2003.
-
J.G.M. Schoenmakers, Accuracy and stability of LIBOR model calibration via parametric correlation structures and approximative swaption pricing, Risk Conference 2002, April 23 - 24, 2002, Paris, France, April 23, 2002.
-
J.G.M. Schoenmakers, Calibration of LIBOR models to caps and swaptions: A way around intrinsic instabilities via parsimonious structures and a collateral market criterion, Johann Wolfgang Goethe-Universität, MathFinance Institute, Frankfurt am Main, November 7, 2002.
-
J.G.M. Schoenmakers, Calibration of LIBOR models to caps and swaptions: A way around intrinsic instabilities via parsimonious structures and a collateral market criterion, Quantitative Finance 2002, Risk Waters Group, London, UK, November 26, 2002.
-
J.G.M. Schoenmakers, Endogenous interest rates in asset markets, 2nd World Congress of the Bachelier Finance Society, June 12 - 15, 2002, Crete, Greece, June 14, 2002.
-
J.G.M. Schoenmakers, Kalibrierung im LIBOR Modell, Reuters AG, Düsseldorf, March 11, 2002.
-
J.G.M. Schoenmakers, Correlation structure in LIBOR market models, calibration to caps and swaptions, Technical University of Delft, Netherlands, May 8, 2001.
-
J.G.M. Schoenmakers, Term structure dynamics endogenously induced by multi-asset markets, Conference Risk 2001 Europe, April 10 - 11, 2001, Paris, France, April 10, 2001.
-
J.G.M. Schoenmakers, HJM term structure dynamics from a multi asset market; finite factor models, Hamburger Stochastik-Tage 2000, March 21 - 24, 2000, Universität Hamburg, March 21, 2000.
-
J.G.M. Schoenmakers, HJM term structure dynamics from a multi asset market; finite factor models, WIAS-Kolloquium, Berlin, May 15, 2000.
-
J.G.M. Schoenmakers, Stable calibration of multi-factor LIBOR market models via a semi-parametric correlation structure, "`ICBI 2000 Conference"', December 6 - 7, 2000, Genf, Switzerland, December 7, 2000.
-
J.G.M. Schoenmakers, Stable implied calibration of multi-factor LIBOR models by semi-parametric correlation structure, Risk Conference Math Week 2000, November 13 - 17, 2000, New York, USA, November 15, 2000.
 External Preprints
External Preprints
-
CH. Bayer, M. Fukasawa, N. Shonosuke , On the weak convergence rate in the discretization of rough volatility models, Preprint no. arXiv:2203.02943, Cornell University, 2022, DOI 10.48550/arXiv.2203.02943 .
-
CH. Bayer, P. Friz, P. Gassiat, J. Martin, B. Stemper , A regularity structure for rough volatility, Preprint no. arXiv:1710.07481, Cornell University Library, arXiv.org, 2017.
Abstract
A new paradigm recently emerged in financial modelling: rough (stochastic) volatility, first observed by Gatheral et al. in high-frequency data, subsequently derived within market microstructure models, also turned out to capture parsimoniously key stylized facts of the entire implied volatility surface, including extreme skews that were thought to be outside the scope of stochastic volatility. On the mathematical side, Markovianity and, partially, semi-martingality are lost. In this paper we show that Hairer's regularity structures, a major extension of rough path theory, which caused a revolution in the field of stochastic partial differential equations, also provides a new and powerful tool to analyze rough volatility models. -
CH. Bayer, B. Veliyev, Utility maximization in a binomial model with transaction costs: A duality approach based on the shadow price process, Preprint no. arXiv:1209.5175, Cornell University Library, arXiv.org, 2012.
-
P. Friz, S. Gerhold, Don't stay local --- Extrapolation analytics for Dupire's local volatility, Preprint no. arXiv:1105.1267, Cornell University Library, arXiv.org, 2011.
-
J.D. Deuschel, P. Friz, A. Jacquier, S. Violante , Marginal density expansions for diffusions and stochastic volatility, Preprint no. arXiv:1111.2462, Cornell University Library, arXiv.org, 2011.
-
J.G.M. Schoenmakers, J. Huang, Optimal dual martingales, their analysis and application to new algorithms for Bermudan products, Preprint no. 1825944, Social Science Research Network (SSRN) Working Paper Series, 2011.
-
J. Kampen, Characteristic functions of affine processes via calculus of their operator symbols, Preprint no. arXiv:1002.2764, Cornell University Library, arXiv.org, 2010.
-
CH. Fries, J. Kampen, On a class of semi-elliptic diffusion models. Part I: A constructive analytical approach for global existence, densities, and numerical schemes with applications to the Libor market model, Preprint no. arXiv:1002.5031, Cornell University Library, arXiv.org, 2010.
-
P. Friz, S. Gerhold, A. Gulisashvili, S. Sturm, On refined volatility smile expansion in the Heston model, Preprint no. arXiv:1001.3003, Cornell University Library, arXiv.org, 2010.
-
R.L. Loeffen, P. Patie, Absolute ruin in the Ornstein--Uhlenbeck type risk model, Preprint no. arXiv:1006.2712, Cornell University Library, arXiv.org, 2010.
Abstract
We start by showing that the finite-time absolute ruin probability in the classical risk model with constant interest force can be expressed in terms of the transition probability of a positive Ornstein-Uhlenbeck type process, say X. Our methodology applies to the case when the dynamics of the aggregate claims process is a subordinator. From this expression, we easily deduce necessary and sufficient conditions for the infinite-time absolute ruin to occur. We proceed by showing that, under some technical conditions, the transition density of X admits a spectral type representation involving merely the limiting distribution of the process. As a by-product, we obtain a series expansions for the finite-time absolute ruin probability. On the way, we also derive, for the aforementioned risk process, the Laplace transform of the first-exit time from an interval from above. Finally, we illustrate our results by detailing some examples. -
N. Serdyukova, Local parametric estimation under noise misspecification in regression, Preprint no. arXiv:0912.4489, Cornell University Library, arXiv.org, 2010.


