One promising way to cope with the new and more complex structures that arise is to exploit probabilistic methods. Indeed, fundamental ansatzes from stochastic geometry (e.g., spatial Poisson processes, continuum percolation theory, ...) are widely used for modelling the spatial locations of the users, the relays and the base stations and their basic connectivity properties. For the description of temporal developments, standard methods from stochastic processes (stochastic interacting particle processes like bootstrap percolation or the contact process) are commonly used to model the spread of large amounts of data through a network.
Contribution of the Institute
The WIAS has started to perform extensive mathematical research on connectivity and capacity problems in mobile relay-augmented probabilistic models over a period of four years within the Leibniz Group "Probabilistic methods for mobile ad-hoc networks" together with the Leibniz-Institute "Innovations for High Performance Microelectronics" (IHP), a major European telecommunications provider and in other collaborations. In recent years the Leibniz junior Research group "Probabilistic Methods for Dynamic Communication Networks" (DYCOMNET) has become WIAS' stronghold for the subject Its expertise includes dynamic modelling of message propagation in dense networks, bottleneck behavior in Device-to-Device (D2D) systems, connection times in large networks without infrastructure, wifi-augmented mobil urban communications models and interference-based spatial analysis of message trajectories as stochastic processes and more.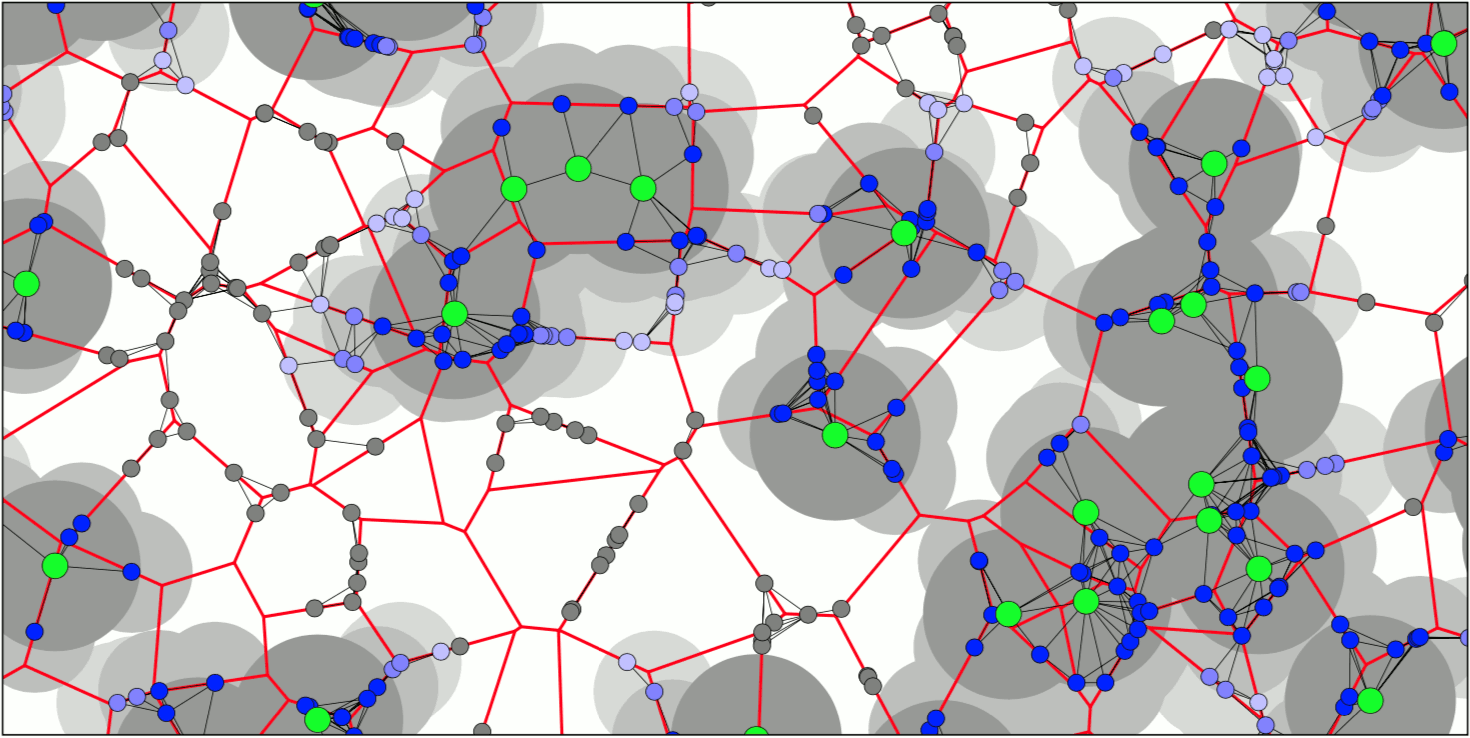
A particular focus is on the simulation and extraction of relevant data, the impact of mobility on key network characteristics, and the possible consequences of delays and buffering of data transfers.

Highlights
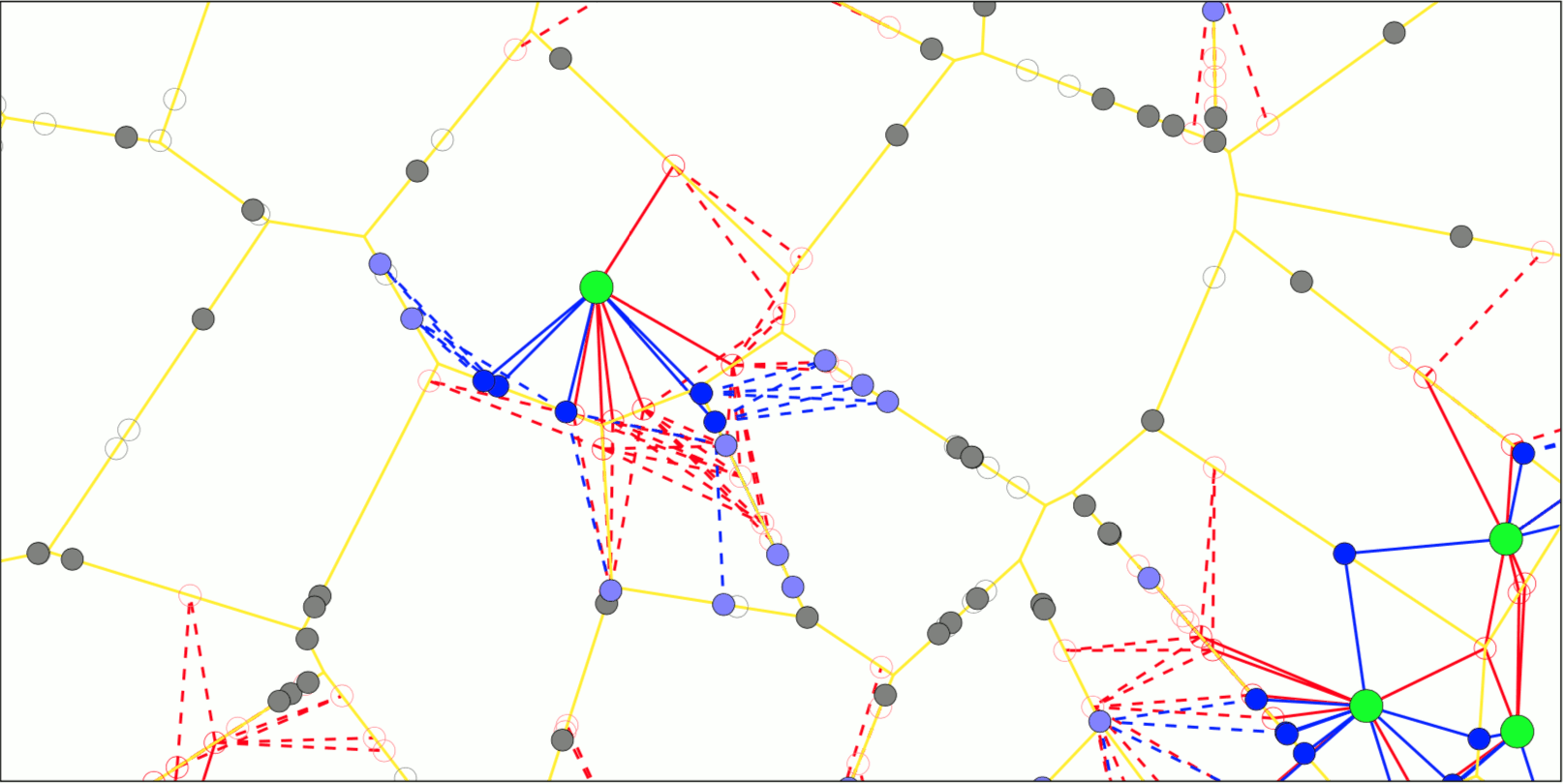
Highlights of recent years include several industry collaborations with a major European telecommunications company aiming to better understand large D2D networks on realistic urban environments which may feature long-range correlations. For example, we were able to demonstrate critical behavior in relation to long-range connections, also called percolation.
Another highlight was the theoretical and numerical investigation of the typical communication cell in random cellular networks based on non-rotationally invariant road systems.
Publications
 Monographs
Monographs
-
B. Jahnel, W. König, Probabilistic Methods in Telecommunications, D. Mazlum, ed., Compact Textbooks in Mathematics, Birkhäuser Basel, 2020, XI, 200 pages, (Monograph Published), DOI 10.1007/978-3-030-36090-0 .
Abstract
This textbook series presents concise introductions to current topics in mathematics and mainly addresses advanced undergraduates and master students. The concept is to offer small books covering subject matter equivalent to 2- or 3-hour lectures or seminars which are also suitable for self-study. The books provide students and teachers with new perspectives and novel approaches. They may feature examples and exercises to illustrate key concepts and applications of the theoretical contents. The series also includes textbooks specifically speaking to the needs of students from other disciplines such as physics, computer science, engineering, life sciences, finance.
 Articles in Refereed Journals
Articles in Refereed Journals
-
A. Hinsen, B. Jahnel, E. Cali, J.-P. Wary, Connectivity in mobile device-to-device networks in urban environments, IEEE Transactions on Information Theory, 69 (2023), pp. 7132--7148, DOI 10.1109/TIT.2023.3298278 .
Abstract
In this article we setup a dynamic device-to-device communication system where devices, given as a Poisson point process, move in an environment, given by a street system of random planar-tessellation type, via a random-waypoint model. Every device independently picks a target location on the street system using a general waypoint kernel, and travels to the target along the shortest path on the streets with an individual velocity. Then, any pair of devices becomes connected whenever they are on the same street in sufficiently close proximity, for a sufficiently long time. After presenting some general properties of the multi-parameter system, we focus on an analysis of the clustering behavior of the random connectivity graph. In our main results we isolate regimes for the almost-sure absence of percolation if, for example, the device intensity is too small, or the connectivity time is too large. On the other hand, we exhibit parameter regimes of sufficiently large intensities of devices, under favorable choices of the other parameters, such that percolation is possible with positive probability. Most interestingly, we also show an in-and-out of percolation as the velocity increases. The rigorous analysis of the system mainly rests on comparison arguments with simplified models via spatial coarse graining and thinning approaches. Here we also make contact to geostatistical percolation models with infinite-range dependencies. -
A. Hinsen, B. Jahnel, E. Cali, J.-P. Wary, Chase-escape in dynamic device-to-device networks, Journal of Applied Probability, published online in August 2023, DOI 10.1017/jpr.2023.47 .
Abstract
The present paper features results on global survival and extinction of an infection in a multi-layer network of mobile agents. Expanding on a model first presented in CHJW22, we consider an urban environment, represented by line-segments in the plane, in which agents move according to a random waypoint model based on a Poisson point process. Whenever two agents are at sufficiently close proximity for a sufficiently long time the infection can be transmitted and then propagates into the system according to the same rule starting from a typical device. Inspired by wireless network architectures, the network is additionally equipped with a second class of agents that is able to transmit a patch to neighboring infected agents that in turn can further distribute the patch, leading to a chase-escape dynamics. We give conditions for parameter configurations that guarantee existence and absence of global survival as well as an in-and-out of the survival regime, depending on the speed of the devices. We also provide complementary results for the setting in which the chase-escape dynamics is defined as an independent process on the connectivity graph. The proofs mainly rest on percolation arguments via discretization and multiscale analysis. -
CH. Hirsch, B. Jahnel, E. Cali, Connection intervals in multi-scale infrastructure-augmented dynamic networks, Stochastic Models, 39 (2023), pp. 851--877, DOI 10.1080/15326349.2023.2184832 .
Abstract
We consider a hybrid spatial communication system in which mobile nodes can connect to static sinks in a bounded number of intermediate relaying hops. We describe the distribution of the connection intervals of a typical mobile node, i.e., the intervals of uninterrupted connection to the family of sinks. This is achieved in the limit of many hops, sparse sinks and growing time horizons. We identify three regimes illustrating that the limiting distribution depends sensitively on the scaling of the time horizon. -
B. Jahnel, S.K. Jhawar, A.D. Vu, Continuum percolation in a nonstabilizing environment, Electronic Journal of Probability, 28 (2023), pp. 131/1--131/38, DOI 10.1214/23-EJP1029 .
Abstract
We prove nontrivial phase transitions for continuum percolation in a Boolean model based on a Cox point process with nonstabilizing directing measure. The directing measure, which can be seen as a stationary random environment for the classical Poisson--Boolean model, is given by a planar rectangular Poisson line process. This Manhattan grid type construction features long-range dependencies in the environment, leading to absence of a sharp phase transition for the associated Cox--Boolean model. Our proofs rest on discretization arguments and a comparison to percolation on randomly stretched lattices established in [MR2116736]. -
B. Jahnel, Ch. Külske, Gibbsianness and non-Gibbsianness for Bernoulli lattice fields under removal of isolated sites, Bernoulli. Official Journal of the Bernoulli Society for Mathematical Statistics and Probability, 29 (2023), pp. 3013--3032, DOI 10.3150/22-BEJ1572 .
Abstract
We consider the i.i.d. Bernoulli field μ p on Z d with occupation density p ∈ [0,1]. To each realization of the set of occupied sites we apply a thinning map that removes all occupied sites that are isolated in graph distance. We show that, while this map seems non-invasive for large p, as it changes only a small fraction p(1-p)2d of sites, there is p(d) <1 such that for all p ∈ (p(d), 1) the resulting measure is a non-Gibbsian measure, i.e., it does not possess a continuous version of its finite-volume conditional probabilities. On the other hand, for small p, the Gibbs property is preserved. -
CH. Hirsch, B. Jahnel, S. Muirhead, Sharp phase transition for Cox percolation, Electronic Communications in Probability, 27 (2022), pp. 48/1--48/13, DOI 10.1214/22-ECP487 .
Abstract
We prove the sharpness of the percolation phase transition for a class of Cox percolation models, i.e., models of continuum percolation in a random environment. The key requirements are that the environment has a finite range of dependence and satisfies a local boundedness condition, however the FKG inequality need not hold. The proof combines the OSSS inequality with a coarse-graining construction. -
B. Jahnel, Ch. Hirsch, E. Cali, Percolation and connection times in multi-scale dynamic networks, Stochastic Processes and their Applications, 151 (2022), pp. 490--518, DOI 10.1016/j.spa.2022.06.008 .
Abstract
We study the effects of mobility on two crucial characteristics in multi-scale dynamic networks: percolation and connection times. Our analysis provides insights into the question, to what extent long-time averages are well-approximated by the expected values of the corresponding quantities, i.e., the percolation and connection probabilities. In particular, we show that in multi-scale models, strong random effects may persist in the limit. Depending on the precise model choice, these may take the form of a spatial birth-death process or a Brownian motion. Despite the variety of structures that appear in the limit, we show that they can be tackled in a common framework with the potential to be applicable more generally in order to identify limits in dynamic spatial network models going beyond the examples considered in the present work. -
B. Jahnel, A. Tóbiás, E. Cali, Phase transitions for the Boolean model of continuum percolation for Cox point processes, Brazilian Journal of Probability and Statistics, 3 (2022), pp. 20--44, DOI 10.1214/21-BJPS514 .
Abstract
We consider the Boolean model with random radii based on Cox point processes. Under a condition of stabilization for the random environment, we establish existence and non-existence of subcritical regimes for the size of the cluster at the origin in terms of volume, diameter and number of points. Further, we prove uniqueness of the infinite cluster for sufficiently connected environments. -
B. Jahnel, A. Tóbiás, SINR percolation for Cox point processes with random powers, Adv. Appl. Math., 54 (2022), pp. 227--253, DOI 10.1017/apr.2021.25 .
Abstract
Signal-to-interference plus noise ratio (SINR) percolation is an infinite-range dependent variant of continuum percolation modeling connections in a telecommunication network. Unlike in earlier works, in the present paper the transmitted signal powers of the devices of the network are assumed random, i.i.d. and possibly unbounded. Additionally, we assume that the devices form a stationary Cox point process, i.e., a Poisson point process with stationary random intensity measure, in two or higher dimensions. We present the following main results. First, under suitable moment conditions on the signal powers and the intensity measure, there is percolation in the SINR graph given that the device density is high and interferences are sufficiently reduced, but not vanishing. Second, if the interference cancellation factor γ and the SINR threshold τ satisfy γ ≥ 1/(2τ), then there is no percolation for any intensity parameter. Third, in the case of a Poisson point process with constant powers, for any intensity parameter that is supercritical for the underlying Gilbert graph, the SINR graph also percolates with some small but positive interference cancellation factor. -
A. Hinsen, B. Jahnel, E. Cali, J.-P. Wary, Phase transitions for chase-escape models on Poisson--Gilbert graphs, Electronic Communications in Probability, 25 (2020), pp. 25/1--25/14, DOI 10.1214/20-ECP306 .
Abstract
We present results on phase transitions of local and global survival in a two-species model on Gilbert graphs. At initial time there is an infection at the origin that propagates on the Gilbert graph according to a continuous-time nearest-neighbor interacting particle system. The Gilbert graph consists of susceptible nodes and nodes of a second type, which we call white knights. The infection can spread on susceptible nodes without restriction. If the infection reaches a white knight, this white knight starts to spread on the set of infected nodes according to the same mechanism, with a potentially different rate, giving rise to a competition of chase and escape. We show well-definedness of the model, isolate regimes of global survival and extinction of the infection and present estimates on local survival. The proofs rest on comparisons to the process on trees, percolation arguments and finite-degree approximations of the underlying random graphs. -
CH. Hirsch, B. Jahnel, A. Tóbiás, Lower large deviations for geometric functionals, Electronic Communications in Probability, 25 (2020), pp. 41/1--41/12, DOI 10.1214/20-ECP322 .
Abstract
This work develops a methodology for analyzing large-deviation lower tails associated with geometric functionals computed on a homogeneous Poisson point process. The technique applies to characteristics expressed in terms of stabilizing score functions exhibiting suitable monotonicity properties. We apply our results to clique counts in the random geometric graph, intrinsic volumes of Poisson--Voronoi cells, as well as power-weighted edge lengths in the random geometric, κ-nearest neighbor and relative neighborhood graph. -
A. Tóbiás, B. Jahnel, Exponential moments for planar tessellations, Journal of Statistical Physics, 179 (2020), pp. 90--109, DOI 10.1007/s10955-020-02521-3 .
Abstract
In this paper we show existence of all exponential moments for the total edge length in a unit disc for a family of planar tessellations based on Poisson point processes. Apart from classical such tessellations like the Poisson--Voronoi, Poisson--Delaunay and Poisson line tessellation, we also treat the Johnson--Mehl tessellation, Manhattan grids, nested versions and Palm versions. As part of our proofs, for some planar tessellations, we also derive existence of exponential moments for the number of cells and the number of edges intersecting the unit disk. -
CH. Hirsch, B. Jahnel, Large deviations for the capacity in dynamic spatial relay networks, Markov Processes and Related Fields, 25 (2019), pp. 33--73.
Abstract
We derive a large deviation principle for the space-time evolution of users in a relay network that are unable to connect due to capacity constraints. The users are distributed according to a Poisson point process with increasing intensity in a bounded domain, whereas the relays are positioned deterministically with given limiting density. The preceding work on capacity for relay networks by the authors describes the highly simplified setting where users can only enter but not leave the system. In the present manuscript we study the more realistic situation where users leave the system after a random transmission time. For this we extend the point process techniques developed in the preceding work thereby showing that they are not limited to settings with strong monotonicity properties. -
W. König, A. Tóbiás, A Gibbsian model for message routeing in highly dense multihop networks, ALEA. Latin American Journal of Probability and Mathematical Statistics, 16 (2019), pp. 211--258, DOI 10.30757/ALEA.v16-08 .
Abstract
We investigate a probabilistic model for routing in relay-augmented multihop ad-hoc communication networks, where each user sends one message to the base station. Given the (random) user locations, we weigh the family of random, uniformly distributed message trajectories by an exponential probability weight, favouring trajectories with low interference (measured in terms of signal-to-interference ratio) and trajectory families with little congestion (measured by how many pairs of hops use the same relay). Under the resulting Gibbs measure, the system targets the best compromise between entropy, interference and congestion for a common welfare, instead of a selfish optimization. We describe the joint routing strategy in terms of the empirical measure of all message trajectories. In the limit of high spatial density of users, we derive the limiting free energy and analyze the optimal strategy, given as the minimizer(s) of a characteristic variational formula. Interestingly, expressing the congestion term requires introducing an additional empirical measure. -
W. König, A. Tóbiás, Routeing properties in a Gibbsian model for highly dense multihop networks, IEEE Transactions on Information Theory, 65 (2019), pp. 6875--6897, DOI 10.1109/TIT.2019.2924187 .
Abstract
We investigate a probabilistic model for routeing in a multihop ad-hoc communication network, where each user sends a message to the base station. Messages travel in hops via the other users, used as relays. Their trajectories are chosen at random according to a Gibbs distribution that favours trajectories with low interference, measured in terms of sum of the signal-to-interference ratios for all the hops, and collections of trajectories with little total congestion, measured in terms of the number of pairs of hops arriving at each relay. This model was introduced in our earlier paper [KT17], where we expressed, in the high-density limit, the distribution of the optimal trajectories as the minimizer of a characteristic variational formula. In the present work, in the special case in which congestion is not penalized, we derive qualitative properties of this minimizer. We encounter and quantify emerging typical pictures in analytic terms in three extreme regimes. We analyze the typical number of hops and the typical length of a hop, and the deviation of the trajectory from the straight line in two regimes, (1) in the limit of a large communication area and large distances, and (2) in the limit of a strong interference weight. In both regimes, the typical trajectory turns out to quickly approach a straight line, in regime (1) with equally-sized hops. Surprisingly, in regime (1), the typical length of a hop diverges logarithmically as the distance of the transmitter to the base station diverges. We further analyze the local and global repulsive effect of (3) a densely populated area on the trajectories. Our findings are illustrated by numerical examples. We also discuss a game-theoretic relation of our Gibbsian model with a joint optimization of message trajectories opposite to a selfish optimization, in case congestion is also penalized -
CH. Hirsch, B. Jahnel, E. Cali, Continuum percolation for Cox point processes, Stochastic Processes and their Applications, 366 (2019), pp. 139--172 (published online on 20.11.2018), DOI 10.1016/j.spa.2018.11.002 .
Abstract
We investigate continuum percolation for Cox point processes, that is, Poisson point processes driven by random intensity measures. First, we derive sufficient conditions for the existence of non-trivial sub- and super-critical percolation regimes based on the notion of stabilization. Second, we give asymptotic expressions for the percolation probability in large-radius, high-density and coupled regimes. In some regimes, we find universality, whereas in others, a sensitive dependence on the underlying random intensity measure survives. -
CH. Hirsch, B. Jahnel, R.I.A. Patterson, Space-time large deviations in capacity-constrained relay networks, ALEA. Latin American Journal of Probability and Mathematical Statistics, 15 (2018), pp. 587--615, DOI 10.30757/ALEA.v15-24 .
Abstract
We consider a single-cell network of random transmitters and fixed relays in a bounded domain of Euclidean space. The transmitters arrive over time and select one relay according to a spatially inhomogeneous preference kernel. Once a transmitter is connected to a relay, the connection remains and the relay is occupied. If an occupied relay is selected by another transmitters with later arrival time, this transmitter becomes frustrated. We derive a large deviation principle for the space-time evolution of frustrated transmitters in the high-density regime. -
CH. Hirsch, B. Jahnel, P. Keeler, R.I.A. Patterson, Large deviations in relay-augmented wireless networks, Queueing Systems. Theory and Applications, 88 (2018), pp. 349--387 (published online on 28.10.2017).
Abstract
We analyze a model of relay-augmented cellular wireless networks. The network users, who move according to a general mobility model based on a Poisson point process of continuous trajectories in a bounded domain, try to communicate with a base station located at the origin. Messages can be sent either directly or indirectly by relaying over a second user. We show that in a scenario of an increasing number of users, the probability that an atypically high number of users experiences bad quality of service over a certain amount of time, decays at an exponential speed. This speed is characterized via a constrained entropy minimization problem. Further, we provide simulation results indicating that solutions of this problem are potentially non-unique due to symmetry breaking. Also two general sources for bad quality of service can be detected, which we refer to as isolation and screening. -
CH. Hirsch, B. Jahnel, P. Keeler, R.I.A. Patterson, Traffic flow densities in large transport networks, Advances in Applied Probability, 49 (2017), pp. 1091--1115, DOI 10.1017/apr.2017.35 .
Abstract
We consider transport networks with nodes scattered at random in a large domain. At certain local rates, the nodes generate traffic flowing according to some navigation scheme in a given direction. In the thermodynamic limit of a growing domain, we present an asymptotic formula expressing the local traffic flow density at any given location in the domain in terms of three fundamental characteristics of the underlying network: the spatial intensity of the nodes together with their traffic generation rates, and of the links induced by the navigation. This formula holds for a general class of navigations satisfying a link-density and a sub-ballisticity condition. As a specific example, we verify these conditions for navigations arising from a directed spanning tree on a Poisson point process with inhomogeneous intensity function. -
CH. Hirsch, B. Jahnel, P. Keeler, R.I.A. Patterson, Large-deviation principles for connectable receivers in wireless networks, Advances in Applied Probability, 48 (2016), pp. 1061--1094.
Abstract
We study large-deviation principles for a model of wireless networks consisting of Poisson point processes of transmitters and receivers, respectively. To each transmitter we associate a family of connectable receivers whose signal-to-interference-and-noise ratio is larger than a certain connectivity threshold. First, we show a large-deviation principle for the empirical measure of connectable receivers associated with transmitters in large boxes. Second, making use of the observation that the receivers connectable to the origin form a Cox point process, we derive a large-deviation principle for the rescaled process of these receivers as the connection threshold tends to zero. Finally, we show how these results can be used to develop importance-sampling algorithms that substantially reduce the variance for the estimation of probabilities of certain rare events such as users being unable to connect. -
P. Keeler, N. Ross, A. Xia, B. Błaszczyszyn, Stronger wireless signals appear more Poisson, IEEE Wireless Communications Letters, 5 (2016), pp. 572--575.
Abstract
Keeler, Ross and Xia [1] recently derived approximation and convergence results, which imply that the point process formed from the signal strengths received by an observer in a wireless network under a general statistical propagation model can be modelled by an inhomogeneous Poisson point process on the positive real line. The basic requirement for the results to apply is that there must be a large number of transmitters with different locations and random propagation effects. The aim of this note is to apply some of the main results of [1] in a less general but more easily applicable form to illustrate how the results can be applied in practice. New results are derived that show that it is the strongest signals, after being weakened by random propagation effects, that behave like a Poisson process, which supports recent experimental work.
[1] P. Keeler, N. Ross, and A. Xia:“When do wireless network signals appear Poisson?? ” -
H. Döring, G. Faraud, W. König, Connection times in large ad-hoc mobile networks, Bernoulli. Official Journal of the Bernoulli Society for Mathematical Statistics and Probability, 22 (2016), pp. 2143--2176.
Abstract
We study connectivity properties in a probabilistic model for a large mobile ad-hoc network. We consider a large number of participants of the system moving randomly, independently and identically distributed in a large domain, with a space-dependent population density of finite, positive order and with a fixed time horizon. Messages are instantly transmitted according to a relay principle, i.e., they are iteratedly forwarded from participant to participant over distances $leq 2R$, with $2R$ the communication radius, until they reach the recipient. In mathematical terms, this is a dynamic continuum percolation model. We consider the connection time of two sample participants, the amount of time over which these two are connected with each other. In the above thermodynamic limit, we find that the connectivity induced by the system can be described in terms of the counterplay of a local, random, and a global, deterministic mechanism, and we give a formula for the limiting behaviour. A prime example of the movement schemes that we consider is the well-known random waypoint model (RWP). Here we describe the decay rate, in the limit of large time horizons, of the probability that the portion of the connection time is less than the expectation. -
P. Keeler, P.G. Taylor, Discussion on ``On the Laplace transform of the aggregate discounted claims with Markovian arrivals'' by Jiandong Ren, Volume 12 (2), North American Actuarial Journal, 19 (2015), pp. 73--77.
-
B. Blaszczyszyn, P. Keeler, Studying the SINR process of the typical user in Poisson networks by using its factorial moment measures, IEEE Transactions on Information Theory, 61 (2015), pp. 6774--6794.
-
B. Blaszczyszyn, M. Karray, P. Keeler, Wireless networks appear Poissonian due to strong shadowing, IEEE Transactions on Wireless Communications, 14 (2015), pp. 4379--4390.
 Contributions to Collected Editions
Contributions to Collected Editions
-
P. Gracar, L. Lüchtrath, Ch. Mönch, The emergence of a giant component in one-dimensional inhomogeneous networks with long-range effects, 18th International Workshop on Algorithms and Models for the Web-Graph, Toronto, Canada, May 23 - 26, 2023, M. Dewar, P. Prałat, P. Szufel, F. Théberge, M. Wrzosek, eds., 13894 of Lecture Notes in Computer Science, Springer, Cham, 2023, pp. 19--35, DOI 10.1007/978-3-031-32296-9_2 .
Abstract
We study the weight-dependent random connection model, a class of sparse graphs featuring many real-world properties such as heavy-tailed degree distributions and clustering. We introduce a coefficient, (deltaf), measuring the effect of the degree-distribution on the occurrence of long edges. We identify a sharp phase transition in (deltaf) for the existence of a giant component in dimension (d=1). -
Z. Benomar, Ch. Ghribi, E. Cali, A. Hinsen, B. Jahnel, Agent-based modeling and simulation for malware spreading in D2D networks, AAMAS '22: Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems, Auckland, New Zealand, May 11 - 13, 2022, International Foundation for Autonomous Agents and Multiagent Systems, Richland, SC, 2022, pp. 91--99.
Abstract
This paper presents a new multi-agent model for simulating malware propagation in device-to-device (D2D) 5G networks. This model allows to understand and analyze mobile malware-spreading dynamics in such highly dynamical networks. Additionally, we present a theoretical study to validate and benchmark our proposed approach for some basic scenarios that are less complicated to model mathematically and also to highlight the key parameters of the model. Our simulations identify critical thresholds for em no propagation and for em maximum malware propagation and make predictions on the malware-spread velocity as well as device-infection rates. To the best of our knowledge, this paper is the first study applying agent-based simulations for malware propagation in D2D. -
CH. Ghribi, E. Cali, Ch. Hirsch, B. Jahnel, Agent-based simulations for coverage extensions in 5G networks and beyond, in: 2022 25th Conference on Innovation in Clouds, Internet and Networks (ICIN), M.F. Zhani, N. Limam, P. Borylo, A. Boubendir, C.R.P. Dos Santos, eds., IEEE, 2022, pp. 1--7, DOI 10.1109/ICIN53892.2022.9758136 .
-
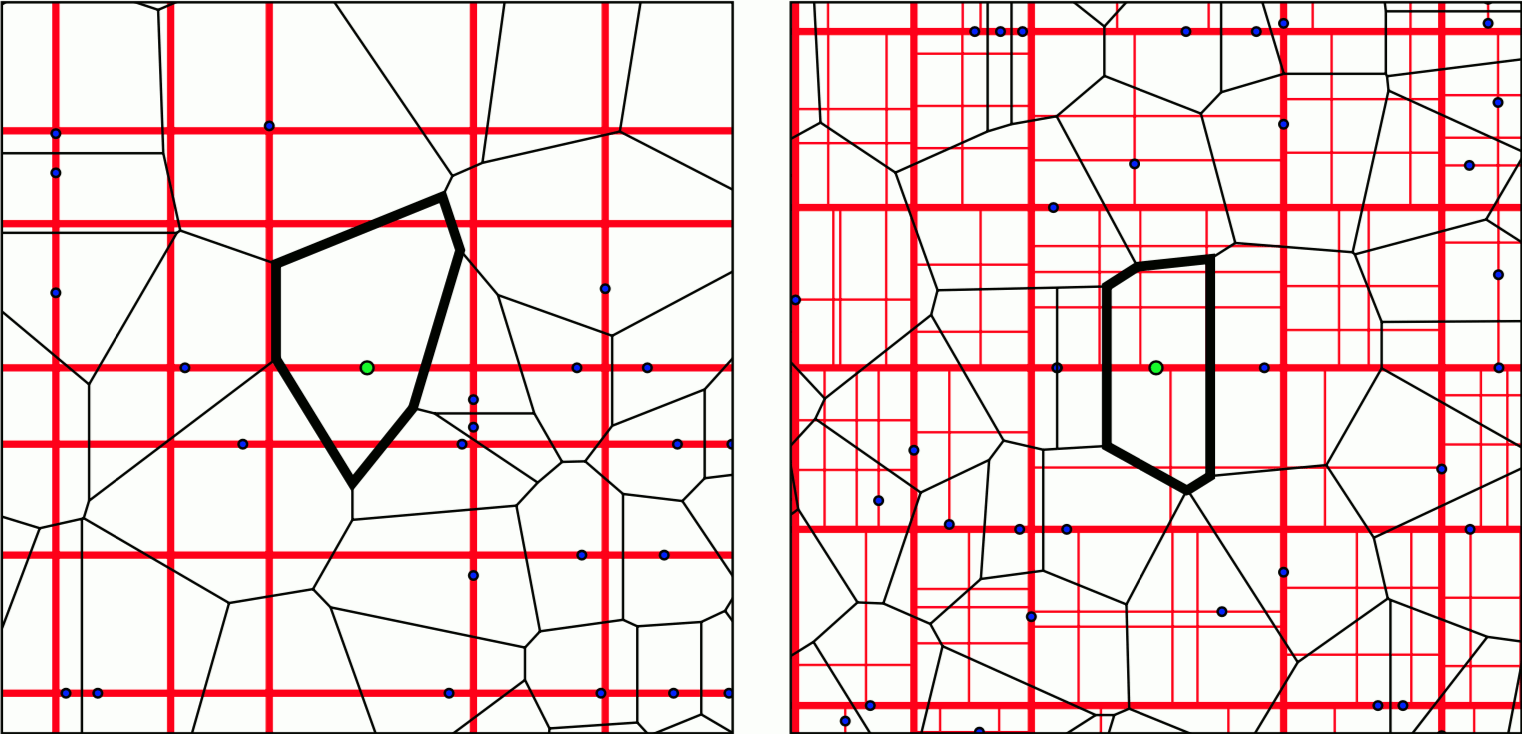
A. Hinsen, Ch. Hirsch, B. Jahnel, E. Cali, Typical Voronoi cells for Cox point processes on Manhatten grids, in: 2019 International Symposium on Modeling and Optimization in Mobile, ad Hoc, and Wireless Networks (WiOPT), Avignon, France, 2019, Institute of Electrical and Electronics Engineers (IEEE), 2020, pp. 1--6, DOI 10.23919/WiOPT47501.2019.9144122 .
Abstract
The typical cell is a key concept for stochastic-geometry based modeling in communication networks, as it provides a rigorous framework for describing properties of a serving zone associated with a component selected at random in a large network. We consider a setting where network components are located on a large street network. While earlier investigations were restricted to street systems without preferred directions, in this paper we derive the distribution of the typical cell in Manhattan-type systems characterized by a pattern of horizontal and vertical streets. We explain how the mathematical description can be turned into a simulation algorithm and provide numerical results uncovering novel effects when compared to classical isotropic networks. -
A. Hinsen, B. Jahnel, E. Cali, J.-P. Wary, Malware propagation in urban D2D networks, in: IEEE 18th International Symposium on on Modeling and Optimization in Mobile, ad Hoc, and Wireless Networks, (WiOpt), Volos, Greece, Institute of Electrical and Electronics Engineers (IEEE), 2020, pp. 1--9.
Abstract
We introduce and analyze models for the propagation of malware in pure D2D networks given via stationary Cox--Gilbert graphs. Here, the devices form a Poisson point process with random intensity measure λ, Λ where Λ is stationary and given, for example, by the edge-length measure of a realization of a Poisson--Voronoi tessellation that represents an urban street system. We assume that, at initial time, a typical device at the center of the network carries a malware and starts to infect neighboring devices after random waiting times. Here we focus on Markovian models, where the waiting times are exponential random variables, and non-Markovian models, where the waiting times feature strictly positive minimal and finite maximal waiting times. We present numerical results for the speed of propagation depending on the system parameters. In a second step, we introduce and analyze a counter measure for the malware propagation given by special devices called white knights, which have the ability, once attacked, to eliminate the malware from infected devices and turn them into white knights. Based on simulations, we isolate parameter regimes in which the malware survives or is eliminated, both in the Markovian and non-Markovian setting. -
B. Jahnel, W. König, Probabilistic methods for spatial multihop communication systems, in: Topics in Applied Analysis and Optimisation, M. Hintermüller, J.F. Rodrigues, eds., CIM Series in Mathematical Sciences, Springer Nature Switzerland AG, Cham, 2019, pp. 239--268.
-
P. Keeler, B. Jahnel, O. Maye, D. Aschenbach, M. Brzozowski, Disruptive events in high-density cellular networks, in: 2018 16th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), IEEE Xplore digital library, 2018, pp. 17789136/1--17789136/8, DOI 10.23919/WIOPT.2018.8362867 .
Abstract
Stochastic geometry models are used to study wireless networks, particularly cellular phone networks, but most of the research focuses on the typical user, often ignoring atypical events, which can be highly disruptive and of interest to network operators. We examine atypical events when a unexpected large proportion of users are disconnected or connected by proposing a hybrid approach based on ray launching simulation and point process theory. This work is motivated by recent results [12] using large deviations theory applied to the signal-to-interference ratio. This theory provides a tool for the stochastic analysis of atypical but disruptive events, particularly when the density of transmitters is high. For a section of a European city, we introduce a new stochastic model of a single network cell that uses ray launching data generated with the open source RaLaNS package, giving deterministic path loss values. We collect statistics on the fraction of (dis)connected users in the uplink, and observe that the probability of an unexpected large proportion of disconnected users decreases exponentially when the transmitter density increases. This observation implies that denser networks become more stable in the sense that the probability of the fraction of (dis)connected users deviating from its mean, is exponentially small. We also empirically obtain and illustrate the density of users for network configurations in the disruptive event, which highlights the fact that such bottleneck behaviour not only stems from too many users at the cell boundary, but also from the near-far effect of many users in the immediate vicinity of the base station. We discuss the implications of these findings and outline possible future research directions.
 Preprints, Reports, Technical Reports
Preprints, Reports, Technical Reports
-
B. Jahnel, U. Rozikov, Gibbs measures for hardcore-SOS models on Cayley trees, Preprint no. 3100, WIAS, Berlin, 2024.
Abstract, PDF (420 kByte)
We investigate the finite-state p-solid-on-solid model, for p=∞, on Cayley trees of order k ≥ 2 and establish a system of functional equations where each solution corresponds to a (splitting) Gibbs measure of the model. Our main result is that, for three states, k=2,3 and increasing coupling strength, the number of translation-invariant Gibbs measures behaves as 1→3 →5 →6 →7. This phase diagram is qualitatively similar to the one observed for three-state p-SOS models with p>0 and, in the case of k=2, we demonstrate that, on the level of the functional equations, the transition p → ∞ is continuous. -
P.P. Ghosh, B. Jahnel, S.K. Jhawar, Large and moderate deviations in Poisson navigations, Preprint no. 3096, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3096 .
Abstract, PDF (318 kByte)
We derive large- and moderate-deviation results in random networks given as planar directed navigations on homogeneous Poisson point processes. In this non-Markovian routing scheme, starting from the origin, at each consecutive step a Poisson point is joined by an edge to its nearest Poisson point to the right within a cone. We establish precise exponential rates of decay for the probability that the vertical displacement of the random path is unexpectedly large. The proofs rest on controlling the dependencies of the individual steps and the randomness in the horizonal displacement as well as renewal-process arguments. -
M. Heida, B. Jahnel, A.D. Vu, An ergodic and isotropic zero-conductance model with arbitrarily strong local connectivity, Preprint no. 3095, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3095 .
Abstract, PDF (377 kByte)
We exhibit a percolating ergodic and isotropic lattice model in all but at least two dimensions that has zero effective conductivity in all spatial directions and for all non-trivial choices of the connectivity parameter. The model is based on the so-called randomly stretched lattice where we additionally elongate layers containing few open edges. -
B. Jahnel, J. Köppl, Time-periodic behaviour in one- and two-dimensional interacting particle systems, Preprint no. 3092, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3092 .
Abstract, PDF (311 kByte)
We provide a class of examples of interacting particle systems on $Z^d$, for $din1,2$, that admit a unique translation-invariant stationary measure, which is not the long-time limit of all translation-invariant starting measures, due to the existence of time-periodic orbits in the associated measure-valued dynamics. This is the first such example and shows that even in low dimensions, not every limit point of the measure-valued dynamics needs to be a time-stationary measure. -
L. Lüchtrath, Ch. Mönch, The directed age-dependent random connection model with arc reciprocity, Preprint no. 3090, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3090 .
Abstract, PDF (304 kByte)
We introduce a directed spatial random graph model aimed at modelling certain aspects of social media networks. We provide two variants of the model: an infinite version and an increasing sequence of finite graphs that locally converge to the infinite model. Both variants have in common that each vertex is placed into Euclidean space and carries a birth time. Given locations and birth times of two vertices, an arc is formed from younger to older vertex with a probability depending on both birth times and the spatial distance of the vertices. If such an arc is formed, a reverse arc is formed with probability depending on the ratio of the endpoints' birth times. Aside from the local limit result connecting the models, we investigate degree distributions, two different clustering metrics and directed percolation. -
B. Jahnel, U. Rozikov, Three-state $p$-SOS models on binary Cayley trees, Preprint no. 3089, WIAS, Berlin, 2024, DOI 10.20347/WIAS.PREPRINT.3089 .
Abstract, PDF (640 kByte)
We consider a version of the solid-on-solid model on the Cayley tree of order two in which vertices carry spins of value 0,1 or 2 and the pairwise interaction of neighboring vertices is given by their spin difference to the power p>0. We exhibit all translation-invariant splitting Gibbs measures (TISGMs) of the model and demonstrate the existence of up to seven such measures, depending on the parameters. We further establish general conditions for extremality and non-extremality of TISGMs in the set of all Gibbs measures and use them to examine selected TISGMs for a small and a large p. Notably, our analysis reveals that extremality properties are similar for large p compared to the case p=1, a case that has been explored already in previous work. However, for the small p, certain measures that were consistently non-extremal for p=1 do exhibit transitions between extremality and non-extremality. -
CH. Hirsch, B. Jahnel, S.K. Jhawar, P. Juhász, Poisson approximation of fixed-degree nodes in weighted random connection models, Preprint no. 3057, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3057 .
Abstract, PDF (474 kByte)
We present a process-level Poisson-approximation result for the degree-$k$ vertices in a high-density weighted random connection model with preferential-attachment kernel in the unit volume. Our main focus lies on the impact of the left tails of the weight distribution for which we establish general criteria based on their small-weight quantiles. To illustrate that our conditions are broadly applicable, we verify them for weight distributions with polynomial and stretched exponential left tails. The proofs rest on truncation arguments and a recently established quantitative Poisson approximation result for functionals of Poisson point processes. -
B. Jahnel, Ch. Külske, A. Zass, Locality properties for discrete and continuum Widom--Rowlinson models in random environments, Preprint no. 3054, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3054 .
Abstract, PDF (606 kByte)
We consider the Widom--Rowlinson model in which hard disks of two possible colors are constrained to a hard-core repulsion between particles of different colors, in quenched random environments. These random environments model spatially dependent preferences for the attach- ment of disks. We investigate the possibility to represent the joint process of environment and infinite-volume Widom--Rowlinson measure in terms of continuous (quasilocal) Papangelou inten- sities. We show that this is not always possible: In the case of the symmetric Widom-Rowlinson model on a non-percolating environment, we can explicitly construct a discontinuity coming from the environment. This is a new phenomenon for systems of continuous particles, but it can be understood as a continuous-space echo of a simpler non-locality phenomenon known to appear for the diluted Ising model (Griffiths singularity random field [ EMSS00]) on the lattice, as we explain in the course of the proof. -
B. Jahnel, J. Köppl, B. Lodewijks, A. Tóbiás, Percolation in lattice k-neighbor graphs, Preprint no. 3028, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3028 .
Abstract, PDF (437 kByte)
We define a random graph obtained via connecting each point of ℤ d independently to a fixed number 1 ≤ k ≤ 2d of its nearest neighbors via a directed edge. We call this graph the emphdirected k-neighbor graph. Two natural associated undirected graphs are the emphundirected and the emphbidirectional k-neighbor graph, where we connect two vertices by an undirected edge whenever there is a directed edge in the directed k-neighbor graph between them in at least one, respectively precisely two, directions. In these graphs we study the question of percolation, i.e., the existence of an infinite self-avoiding path. Using different kinds of proof techniques for different classes of cases, we show that for k=1 even the undirected k-neighbor graph never percolates, but the directed one percolates whenever k≥ d+1, k≥ 3 and d ≥5, or k ≥4 and d=4. We also show that the undirected 2-neighbor graph percolates for d=2, the undirected 3-neighbor graph percolates for d=3, and we provide some positive and negative percolation results regarding the bidirectional graph as well. A heuristic argument for high dimensions indicates that this class of models is a natural discrete analogue of the k-nearest-neighbor graphs studied in continuum percolation, and our results support this interpretation. -
P. Gracar, L. Lüchtrath, Ch. Mönch, The emergence of a giant component in one-dimensional inhomogeneous networks with long-range effects, Preprint no. 3011, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3011 .
Abstract, PDF (5064 kByte)
We study the weight-dependent random connection model, a class of sparse graphs featuring many real-world properties such as heavy-tailed degree distributions and clustering. We introduce a coefficient, (deltaf), measuring the effect of the degree-distribution on the occurrence of long edges. We identify a sharp phase transition in (deltaf) for the existence of a giant component in dimension (d=1). -
B. Jahnel, J. Köppl, On the long-time behaviour of reversible interacting particle systems in one and two dimensions, Preprint no. 3004, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.3004 .
Abstract, PDF (287 kByte)
By refining Holley's free energy technique, we show that, under quite general assumptions on the dynamics, the attractor of a (possibly non-translation-invariant) interacting particle system in one or two spatial dimensions is contained in the set of Gibbs measures if the dynamics admits a reversible Gibbs measure. In particular, this implies that there can be no reversible interacting particle system that exhibits time-periodic behaviour and that every reversible interacting particle system is ergodic if and only if the reversible Gibbs measure is unique. In the special case of non-attractive stochastic Ising models this answers a question due to Liggett. -
B. Jahnel, L. Lüchtrath, Existence of subcritical percolation phases for generalised weight-dependent random connection models, Preprint no. 2993, WIAS, Berlin, 2023, DOI 10.20347/WIAS.PREPRINT.2993 .
Abstract, PDF (299 kByte)
We derive a sufficient condition for the existence of a subcritical percolation phase for a wide range of continuum percolation models where each vertex is embedded into Euclidean space and carries an independent weight. In contrast to many established models, the presence of an edge is not only allowed to depend on the distance and weights of its end vertices but can also depend on the surrounding vertex set. Our result can be applied in particular to models combining heavy-tailed degree distributions and long-range effects, which are typically well connected. Moreover, we establish bounds on the tail-distribution of the number of points and the diameter of the subcritical component of a typical point. The proofs rest on a multi-scale argument. -
Z. Benomar, Ch. Ghribi, E. Cali, A. Hinsen, B. Jahnel, J.-P. Wary, Multi-agent simulations for virus propagation in D2D 5G+ networks, Preprint no. 2953, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2953 .
Abstract, PDF (367 kByte)
In this paper we present results for an extended class of multi-agent simulation models for malware propagation in device-to-device 5G networks, first exhibited in citeAgentBasedAAMAS. The models allow to understand and analyze mobile malware spreading dynamics in highly dynamical networks and also to assess the effectiveness of a proposed counter measure policy for reversing attacks and securing the system. Our main simulation studies identify critical thresholds for maximal malware propagation and isolate two distinguished regimes for malware survival and extermination depending on a variety of parameters. We further predict via simulations the malware spreading velocities, depending on device density and speed, as well as the percentage of counter agents that have to be introduced into the network for malware elimination. We complement these findings and state also an associated theoretical study that highlights the key parameters of our agent-based model and exhibit certain linear relationships between them [1]. -
CH. Ghribi, E. Cali, Ch. Hirsch, B. Jahnel, Agent-based simulations for coverage extensions in 5G networks and beyond, Preprint no. 2920, WIAS, Berlin, 2022, DOI 10.20347/WIAS.PREPRINT.2920 .
Abstract, PDF (1032 kByte)
Device-to-device (D2D) communications is one of the key emerging technologies for the fifth generation (5G) networks and beyond. It enables direct communication between mobile users and thereby extends coverage for devices lacking direct access to the cellular infrastructure and hence enhances network capacity. D2D networks are complex, highly dynamic and will be strongly augmented by intelligence for decision making at both the edge and core of the network, which makes them particularly difficult to predict and analyze. Conventionally, D2D systems are evaluated, investigated and analyzed using analytical and probabilistic models (e.g., from stochastic geometry). However, applying classical simulation and analytical tools to such a complex system is often hard to track and inaccurate. In this paper, we present a modeling and simulation framework from the perspective of complex-systems science and exhibit an agent-based model for the simulation of D2D coverage extensions. We also present a theoretical study to benchmark our proposed approach for a basic scenario that is less complicated to model mathematically. Our simulation results show that we are indeed able to predict coverage extensions for multi-hop scenarios and quantify the effects of street-system characteristics and pedestrian mobility on the connection time of devices to the base station (BS). To our knowledge, this is the first study that applies agent-based simulations for coverage extensions in D2D.
 Talks, Poster
Talks, Poster
-
A. Zass, The statistical mechanics of the interlacement point process, Second Annual Conference of the SPP2265, March 27 - 30, 2023, Deutsches Zentrum für Luft- und Raumfahrt (DLR), Köln, March 30, 2023.
-
B. Jahnel, Continuum percolation in random environment, Oberseminar zur Stochastik, Otto-von-Guericke-Universität Magdeburg, Fakultät für Mathematik, June 22, 2023.
-
B. Jahnel, Dynamical Gibbs variational principles and attractor properties, Mathematisches Kolloquium, Universität zu Köln, Abteilung Mathematik, June 14, 2023.
-
B. Jahnel, Percolation, Oberseminar, Technische Universität Braunschweig, Institut für Mathematische Stochastik, November 8, 2023.
-
B. Jahnel, Stochastische Methoden für Kommunikationsnetzwerke, Seminar der Fakultät Informatik, Hochschule Reutlingen, October 6, 2023.
-
B. Jahnel, Stochastische Methoden für Kommunikationsnetzwerke, Orientierungsmodul der Technischen Universität Braunschweig, Institut für Mathematische Stochastik, November 2, 2023.
-
B. Jahnel, Stochastische Methoden für Kommunikationsnetzwerke, Orientierungsmodul der Technischen Universität Braunschweig, Institut für Mathematische Stochastik, January 30, 2023.
-
B. Jahnel, Subcritical percolation phases for generalized weight-dependent random connection models, 21st INFORMS Applied Probability Society Conference, June 28 - 30, 2023, Centre Prouvé, Nancy, France, June 29, 2023.
-
B. Jahnel, The statistical mechanics of the interlacement point process, Second Annual Conference of the SPP 2265, March 27 - 30, 2023, Deutsches Zentrum für Luft- und Raumfahrt (DLR), Köln, March 29, 2023.
-
B. Jahnel, Subcritical percolation phases for generalized weight-dependent random connection models, DMV Annual Meeting 2023, Minisymposium MS 12 ``Random Graphs and Statistical Network Analysis'', September 25 - 28, 2023, Technische Universität Ilmenau, September 25, 2023.
-
W. König, The statistical mechanics of the interlacement point process, Second Annual Conference of the SPP 2265, March 27 - 30, 2023, Deutsches Zentrum für Luft- und Raumfahrt (DLR), Köln, March 30, 2023.
-
L. Lüchtrath, Evolving networks, their limits and global properties, Oberseminar Stochastik, Universität Augsburg, Institut für Mathematik, January 25, 2023.
-
B. Jahnel, Malware propagation in mobile device-to-device networks (online talk), Joint H2020 AI@EDGE and INSPIRE-5G Project Workshop -- Platforms and Mathematical Optimization for Secure and Resilient Future Networks (Online Event), Paris, France, November 8 - 9, 2022, November 8, 2022.
-
B. Jahnel, Phase transitions and large deviations for the Boolean model of continuum percolation for Cox point processes (online talk), Probability Seminar University Padua, Università di Padova, Dipartimento di Matematica, Italy, March 25, 2022.
-
B. Jahnel, Stochastic geometry for telecommunications, Leibniz MMS Days 2022, April 25 - 27, 2022, Potsdam-Institut für Klimafolgenforschung (PIK), April 26, 2022.
-
B. Jahnel, Connectivity improvements in mobile device-to-device networks (online talk), Telecom Orange Paris, France, July 6, 2021.
-
B. Jahnel, First-passage percolation and chase-escape dynamics on random geometric graphs, Stochastic Geometry Days, November 15 - 19, 2021, Dunkerque, France, November 17, 2021.
-
B. Jahnel, Phase transitions for the Boolean model for Cox point processes, Workshop on Randomness Unleashed Geometry, Topology, and Data, September 22 - 24, 2021, University of Groningen, Faculty of Science and Engineering, Groningen, Netherlands, September 23, 2021.
-
B. Jahnel, Phase transitions for the Boolean model for Cox point processes (online talk), DYOGENE Seminar (Online Event), INRIA Paris, France, January 11, 2021.
-
B. Jahnel, Phase transitions for the Boolean model for Cox point processes (online talk), Probability Seminar Bath (Online Event), University of Bath, Department of Mathematical Sciences, UK, October 18, 2021.
-
W. König, A box version of the interacting Bose gas, Workshop on Randomness Unleashed Geometry, Topology, and Data, September 22 - 24, 2021, University of Groningen, Faculty of Science and Engineering, Groningen, Netherlands, September 23, 2021.
-
B. Jahnel, Phase transitions for the Boolean model for Cox point processes (online talk), Bernoulli-IMS One World Symposium 2020 (Online Event), August 24 - 28, 2020, August 27, 2020.
-
A. Hinsen, Data mobility in ad-hoc networks: Vulnerability and security, KEIN öffentlicher Vortrag (Orange), Telecom Orange Paris, France, December 12, 2019.
-
A. Hinsen, IPS in telecommunication I, Workshop on Probability, Analysis and Applications (PAA), September 23 - October 4, 2019, African Institute for Mathematical Sciences --- Ghana (AIMS Ghana), Accra, October 4, 2019.
-
A. Hinsen, IPS in telecommunication II, Workshop on Probability, Analysis and Applications (PAA), September 23 - October 4, 2019, African Institute for Mathematical Sciences --- Ghana (AIMS Ghana), Accra, October 4, 2019.
-
A. Hinsen, Introduction to interacting particles systems (IPS), Workshop on Probability, Analysis and Applications (PAA), September 23 - October 4, 2019, African Institute for Mathematical Sciences --- Ghana (AIMS Ghana), Accra, October 2, 2019.
-
A. Hinsen, The White Knight model --- An epidemic on a spatial random network, Bocconi Summer School in Advanced Statistics and Probability, Lake Como School of Advanced Studies, Lake Como, Italy, July 8 - 19, 2019.
-
B. Jahnel, Continuum percolation in random environment, Workshop on Probability, Analysis and Applications (PAA), September 23 - October 4, 2019, African Institute for Mathematical Sciences --- Ghana (AIMS Ghana), Accra.
-
A. Hinsen, Random Malware Propagation, MATH+ Center Days 2018, October 31 - November 2, 2018, Zuse-Institut Berlin (ZIB), Berlin, October 31, 2018.
-
B. Jahnel, Telecommunication models in random environments, BIMoS Day : The Mathematics of Quantum Information, May 23, 2018, Technische Universität Berlin, Berlin, May 23, 2018.
-
W. König, Probabilistic Methods in Telecommunication, MATH+ Center Days 2018, October 31 - November 2, 2018, Zuse-Institut Berlin (ZIB), Berlin, October 31, 2018.
-
A. Wapenhans, Data mobility in ad-hoc networks: Vulnerability & security, Telecom Orange Paris, France, November 17, 2017.
-
B. Jahnel, Continuum percolation for Cox processes, Seminar, Ruhr Universität Bochum, Fakultät für Mathematik, October 27, 2017.
-
B. Jahnel, Continuum percolation theory applied to Device to Device, Telecom Orange Paris, France, November 17, 2017.
-
B. Jahnel, Stochastic geometry in telecommunications, Summer School 2017: Probabilistic and Statistical Methods for Networks, August 21 - September 1, 2017, Technische Universität Berlin, Berlin Mathematical School.
-
CH. Hirsch, Large deviations in relay-augmented wireless networks, Workshop on Dynamical Networks and Network Dynamics, January 17 - 22, 2016, International Centre for Mathematical Science, Edinburgh, UK, January 18, 2016.
-
P. Keeler, Signal-to-interference ratio in wireless communication networks, Workshop on Dynamical Networks and Network Dynamics, January 17 - 24, 2016, International Centre for Mathematical Science, Edinburgh, UK, January 18, 2016.
-
W. König, Connection times in large ad-hoc mobile networks, Workshop on Dynamical Networks and Network Dynamics, January 18 - 21, 2016, International Centre for Mathematical Science, Edinburgh, UK, January 18, 2016.
-
P. Keeler, Large-deviation theory and coverage in mobile phone networks, Seminar ``Applied Probability'', The University of Melbourne, Department of Mathematics and Statistics, Australia, August 17, 2015.
-
P. Keeler, The Poisson--Dirichlet process and coverage in mobile phone networks, Stochastic Processes and Special Functions Workshop, August 13 - 14, 2015, The University of Melbourne, Melbourne, Australia, August 14, 2015.
-
P. Keeler, When do wireless network signals appear Poisson?, Simons Conference on Networks and Stochastic Geometry, May 18 - 21, 2015, University of Texas, Austin, USA, May 20, 2015.
-
G. Faraud, Connection times in large ad-hoc networks, Ecole de Printemps ``Marches Aléatoires, Milieux Aléatoires, Renforcements'' (MEMEMO2), June 10 - 14, 2013, Aussois, France, June 13, 2013.
 External Preprints
External Preprints
-
N. Djurdjevac Conrad, J. Köppl, A. Djurdjevac, Feedback loops in opinion dynamics of agent-based models with multiplicative noise, Preprint no. arXiv:2209.07151, Cornell University, 2022, DOI 10.48550/arXiv.2209.07151 .
Abstract
We introduce an agent-based model for co-evolving opinion and social dynamics, under the influence of multiplicative noise. In this model, every agent is characterized by a position in a social space and a continuous opinion state variable. Agents? movements are governed by positions and opinions of other agents and similarly, the opinion dynamics is influenced by agents? spatial proximity and their opinion similarity. Using numerical simulations and formal analysis, we study this feedback loop between opinion dynamics and mobility of agents in a social space. We investigate the behavior of this ABM in different regimes and explore the influence of various factors on appearance of emerging phenomena such as group formation and opinion consensus. We study the empirical distribution and in the limit of infinite number of agents we derive a corresponding reduced model given by a partial differential equation (PDE). Finally, using numerical examples we show that a resulting PDE model is a good approximation of the original ABM.