A descent method for the free energy of multicomponent
systems
Collaborator: H. Gajewski (FG 1),
J.A. Griepentrog (FG 1),
K. Gärtner (FG 3)
Cooperation with: J. Beuthan, O. Minet
(Charité, Institut für Medizinische Physik und Lasermedizin, Berlin)
Supported by: BMBF-Verbundprojekt: ,,Anwendung eines nichtlokalen
Phasenseparationsmodells zur Bildbewertung in der Rheumadiagnostik''
(Joint Project: Application of a nonlocal phase separation model to
optical diagnosis of rheumatic diseases)
Description:
To describe phase-separation processes, we consider a closed system with
interacting particles of type
i  {0, 1,..., m} occupying a spatial
Lipschitz domain
{0, 1,..., m} occupying a spatial
Lipschitz domain
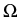
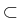
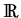 n.
We assume that the particles jump around on a given
microscopically scaled lattice following a stochastic exchange process.
Exactly one particle sits on each lattice
site (exclusion principle).
Two particles of type i and
n.
We assume that the particles jump around on a given
microscopically scaled lattice following a stochastic exchange process.
Exactly one particle sits on each lattice
site (exclusion principle).
Two particles of type i and 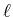 change their sites x and y with
a certain probability
pi
change their sites x and y with
a certain probability
pi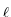 (x, y) due to diffusion and
interaction. The hydrodynamical limit (see [2])
leads to a system of m + 1 conservation laws:
(x, y) due to diffusion and
interaction. The hydrodynamical limit (see [2])
leads to a system of m + 1 conservation laws:
ui' +  . ji = 0 in
(0, T) x . ji = 0 in
(0, T) x 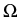 , ,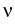 . ji = 0 on
(0, T) x . ji = 0 on
(0, T) x 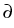 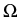 , ui(0) = u0i in , ui(0) = u0i in 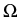 , ,
|
(1) |
with mass densities
u0,..., um,
their initial values
u00,..., u0m,
and current densities
j0,..., jm.
Due to the exclusion principle, we can assume
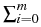 ui = 1,
ui = 1,
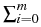 u0i = 1, and
u0i = 1, and
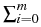 ji = 0.
Hence, we can describe the state of the system by
u = (u1,..., um) and
u0 = 1 -
ji = 0.
Hence, we can describe the state of the system by
u = (u1,..., um) and
u0 = 1 - 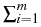 ui.
ui.
Equilibrium distributions
u* = (u1*,..., um*) : 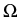
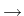
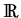 m of the multicomponent system, and more generally,
steady states of the evolution system can be supposed to be
local minimizers of the free energy functional F
under the constraint of mass conservation:
m of the multicomponent system, and more generally,
steady states of the evolution system can be supposed to be
local minimizers of the free energy functional F
under the constraint of mass conservation:
F(
u*) = min
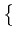 F
F(
u) :
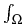
(
ui -
u0i) d
x = 0
for
i 
{1,...,
m}
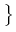
,
or solutions
(u*,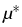 ) of the Euler-Lagrange
equations including Lagrange multipliers
) of the Euler-Lagrange
equations including Lagrange multipliers
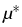

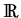 m:
m:
DF(u*) = 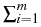 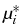 gi, gi,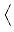 gi, u gi, u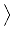 = = 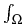 ui dx, ui dx,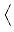 gi, u* - u0 gi, u* - u0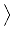 = 0, i = 0, i  {1,..., m}. {1,..., m}.
|
(2) |
In many applications, one is originally interested in u*.
However, F is in general not convex,
so it seems to be difficult to solve (2) directly.
One can try to construct u* as steady state of the evolution
system (1): In view of the fact that the Lagrange multipliers
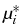 should be constant, one assumes their antigradients to be driving
forces towards equilibrium.
This leads to the evolution system (1) with current densities
ji = -
should be constant, one assumes their antigradients to be driving
forces towards equilibrium.
This leads to the evolution system (1) with current densities
ji = - 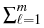 ai
ai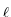 (u)
(u)
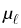 and positively
semidefinite mobility matrix
(ai
and positively
semidefinite mobility matrix
(ai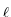 )
(see [2], [3]).
Evidently, F is a Lyapunov function of (1),
and the authors have developed a dissipative discretization scheme
with respect to space and time. However, from the practical point of view
that approach becomes questionable if meta-stable states occur.
Hence, we want to establish a descent method to solve (2)
directly (see [1]):
)
(see [2], [3]).
Evidently, F is a Lyapunov function of (1),
and the authors have developed a dissipative discretization scheme
with respect to space and time. However, from the practical point of view
that approach becomes questionable if meta-stable states occur.
Hence, we want to establish a descent method to solve (2)
directly (see [1]):
To formulate our problem, we use standard
spaces
H = L2(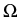 ;
;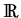 m) and
V = L
m) and
V = L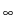 (
(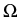 ;
;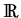 m).
We consider the decomposition of
H = H0 + H1 into the closed subspace
H0 = {u
m).
We consider the decomposition of
H = H0 + H1 into the closed subspace
H0 = {u  H :
H : 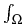 u dx = 0}
and the m-dimensional subspace
H1
u dx = 0}
and the m-dimensional subspace
H1 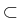 V of constants.
Let
J
V of constants.
Let
J 
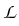 (H;H*) be the duality map between H and H*.
Then the annihilator
H00 = J[H1] is the m-dimensional subspace
of elements
f =
(H;H*) be the duality map between H and H*.
Then the annihilator
H00 = J[H1] is the m-dimensional subspace
of elements
f = 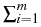
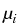 gi where
gi where
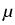

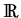 m and
g1,..., gm
m and
g1,..., gm  J[V] are given by
J[V] are given by
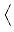 gi, u
gi, u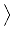 =
= 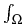 ui dx, u
ui dx, u  H.
H.
We split the free energy functional
F : H 
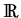
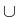 { +
{ + 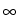 } into a sum
F =
} into a sum
F = 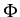 +
+ 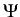 of a chemical part
of a chemical part
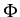 : H
: H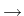
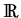
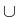 { +
{ + 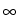 }
and a nonlocal interaction part
}
and a nonlocal interaction part
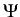 : H
: H 
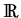 as follows:
as follows:
We introduce a lower semicontinuous and strongly convex functional
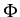 : H
: H 
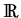
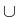 { +
{ + 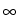 } by
} by
where
dom(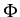 ) = {u
) = {u  H : 0
H : 0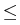 u0, u1,..., um
u0, u1,..., um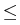 1}
and
dom(
1}
and
dom(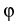 ) = {z
) = {z 
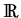 m : 0
m : 0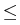 z0, z1,..., zm
z0, z1,..., zm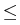 1}.
Additionally, we fix
l
1}.
Additionally, we fix
l  J[V] and
d
J[V] and
d 
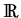 and define
a quadratic functional
and define
a quadratic functional
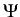 : H
: H 
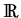 by
by
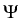 (u) = (u) = 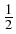 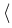 Tu, u Tu, u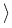 + + 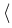 l, u l, u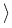 + d, u + d, u  H, H,
|
(4) |
where
T 
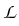 (H;H*) is a self-adjoint and completely
continuous operator such that T| V is a completely
continuous operator in
(H;H*) is a self-adjoint and completely
continuous operator such that T| V is a completely
continuous operator in
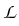 (V;J[V]). Then we can find constants
(V;J[V]). Then we can find constants
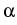 ,
, 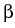 > 0 such that
> 0 such that
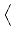
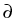
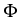
(
u) -
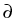
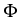
(
v),
u -
v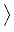
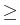
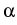
|
u -
v|
2H,|
D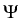
(
u) -
D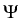
(
v)|
H*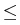
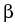
|
u -
v|
H,
u,
v 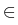
dom(
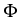
).
If we specify
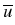
 int dom(
int dom(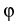 )
and the set
K =
)
and the set
K = 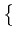 u
u  dom(
dom(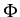 ) :
) : 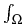 (u -
(u - 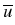 ) dx = 0
) dx = 0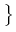 of mass constraints,
then the functional
F : H
of mass constraints,
then the functional
F : H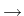
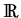
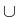 { +
{ + 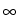 } is bounded from
below, and there exists a solution u*
} is bounded from
below, and there exists a solution u*  K of the constrained
minimum problem
F(u*) = min
K of the constrained
minimum problem
F(u*) = min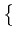 F(u) : u
F(u) : u  K
K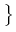 .
.
In view of the above assumptions on monotonicity, continuity, and compactness,
we can find convex subsets
C 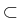 K and
M
K and
M 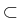 H00
which are closed in V and J[V], respectively,
such that for all initial values u0
H00
which are closed in V and J[V], respectively,
such that for all initial values u0  K, we can define iteration
sequences
(uk)
K, we can define iteration
sequences
(uk) 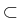 K and
(vk, fk)
K and
(vk, fk)  C x M by
C x M by
uk+1 = 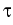 vk + (1 - vk + (1 - 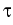 )uk, fk )uk, fk 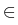 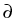 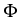 (vk) + D (vk) + D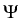 (uk), k (uk), k 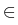 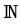 . .
|
(5) |
Here, the relaxation parameter
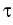
 (0, 1] satisfies
(0, 1] satisfies
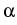 >
> 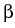
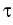 which ensures the decay and the convergence
of (F(uk)) due to the descent property
which ensures the decay and the convergence
of (F(uk)) due to the descent property
|
uk -
uk+1|
H2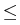
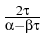
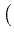 F
F(
uk) -
F(
uk+1)
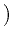
,
k 
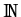
.
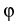 , we can apply
a
, we can apply
a 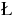 ojasiewicz-Simon-type inequality to prove
that the sequence
(uk, fk)
ojasiewicz-Simon-type inequality to prove
that the sequence
(uk, fk) 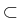 K x M defined by (5)
converges to a solution
(u*, f*)
K x M defined by (5)
converges to a solution
(u*, f*)  C x M
of the Euler-Lagrange equation (see (2))
in the sense of
C x M
of the Euler-Lagrange equation (see (2))
in the sense of
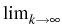 F(uk) = F(u*),
F(uk) = F(u*),
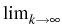 | uk - u*|V = 0,
and
| uk - u*|V = 0,
and
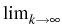 | fk - f*|J[V] = 0.
| fk - f*|J[V] = 0.
To apply our descent method to image processing, we describe the
nonlocal interaction by means of inverse operators corresponding
to second-order elliptic operators with appropriate regularity properties.
To do so, for r > 0 we consider the family of elliptic operators
Er 
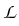
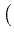 H1(
H1(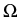 );H1(
);H1(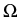 )*
)*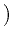 (including Neumann boundary conditions) given by
(including Neumann boundary conditions) given by
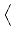 Erv
Erv,
h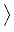
=
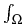
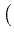 r2
r2 v .
v .  h
h +
vh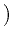
d
x,
v,
h  H1
H1(
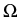
).
We want to emphasize that the inverse
Er-1 
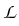
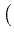 H1(
H1(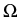 )*;H1(
)*;H1(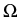 )
)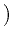 is completely continuous from
L2(
is completely continuous from
L2(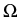 ) into
L2(
) into
L2(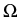 )
as well as from
L
)
as well as from
L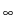 (
(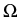 ) into
L
) into
L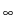 (
(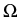 ).
).
To control the qualitative behavior of nonlocal interaction, we prescribe
effective ranges 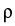 , r > 0 and intensities
, r > 0 and intensities
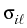 ,
si
,
si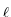

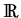 of interaction forces
between particles of type i and
of interaction forces
between particles of type i and
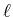
 {0, 1,..., m}, respectively.
Clearly, both matrices
(
{0, 1,..., m}, respectively.
Clearly, both matrices
(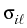 ) and
(si
) and
(si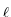 ) are assumed
to be symmetric. The cases
) are assumed
to be symmetric. The cases
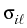 > 0 and
> 0 and
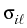 < 0
represent repulsive and attractive interaction, respectively.
The nontrivial choice of
(si
< 0
represent repulsive and attractive interaction, respectively.
The nontrivial choice of
(si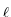 ) enables us
to get final states close to the corresponding initial values u0
) enables us
to get final states close to the corresponding initial values u0  K
if we define the quadratic functional
K
if we define the quadratic functional
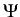 : H
: H 
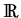 according to (4):
according to (4):
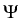
(
u) =
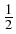
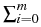
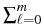
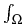
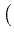 ui
ui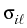 E
E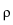 -1u
-1u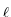
+ (
ui -
u0i)
si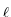 Er-1
Er-1(
u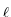
-
u0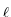
)
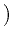
d
x,
u  H
H.
In our joint BMBF project, we use the above nonlocal image segmentation method
to analyze medical images regarding the scattering light distribution of the
near-infrared spectral range on rheumatoid finger joints.
Rheumatoid arthritis is the most common inflammatory arthropathy;
it often affects the small joints, especially the finger joints.
Inflammation of joints caused by rheumatic diseases starts with
an inflammatory process of capsule synovial structures.
Later, granulation tissue develops in the synovialis
and destroys the cartilage and even the bone structure.
Figures 1 and 2 show two examples of healthy and rheumatoid finger joints
and the corresponding results of image segmentation with respect to three
components (bone, cartilage, and synovial fluid):
Fig. 1:
Healthy finger joint
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.3\textwidth}{gesund.eps}{gesund2.eps}
\makeatother](img841.gif) |
Fig. 2:
Rheumatoid finger joint
![\makeatletter
\@ZweiProjektbilderNocap[h]{0.3\textwidth}{krank.eps}{krank2.eps}
\makeatother](img842.gif) |
References:
- H. GAJEWSKI, J.A. GRIEPENTROG,
A descent method for the free energy of multicomponent systems,
WIAS Preprint no. 980, 2004
.
- G. GIACOMIN, J.L. LEBOWITZ, R. MARRA,
Macroscopic evolution of particle systems
with short- and long-range interactions,
Nonlinearity, 13 (2000), pp. 2143-2162.
- J.A. GRIEPENTROG,
On the unique solvability of
a phase separation problem for multicomponent systems,
Banach Center Publ., 66 (2004), pp. 153-164.
LaTeX typesetting by H. Pletat
2005-07-29
![]() {0, 1,..., m} occupying a spatial
Lipschitz domain
{0, 1,..., m} occupying a spatial
Lipschitz domain
![]()
![]()
![]() n.
We assume that the particles jump around on a given
microscopically scaled lattice following a stochastic exchange process.
Exactly one particle sits on each lattice
site (exclusion principle).
Two particles of type i and
n.
We assume that the particles jump around on a given
microscopically scaled lattice following a stochastic exchange process.
Exactly one particle sits on each lattice
site (exclusion principle).
Two particles of type i and ![]() change their sites x and y with
a certain probability
pi
change their sites x and y with
a certain probability
pi![]() (x, y) due to diffusion and
interaction. The hydrodynamical limit (see [2])
leads to a system of m + 1 conservation laws:
(x, y) due to diffusion and
interaction. The hydrodynamical limit (see [2])
leads to a system of m + 1 conservation laws:
![]()
![]()
![]() m of the multicomponent system, and more generally,
steady states of the evolution system can be supposed to be
local minimizers of the free energy functional F
under the constraint of mass conservation:
m of the multicomponent system, and more generally,
steady states of the evolution system can be supposed to be
local minimizers of the free energy functional F
under the constraint of mass conservation:
![]() ;
;![]() m) and
V = L
m) and
V = L![]() (
(![]() ;
;![]() m).
We consider the decomposition of
H = H0 + H1 into the closed subspace
H0 = {u
m).
We consider the decomposition of
H = H0 + H1 into the closed subspace
H0 = {u ![]() H :
H : ![]() u dx = 0}
and the m-dimensional subspace
H1
u dx = 0}
and the m-dimensional subspace
H1 ![]() V of constants.
Let
J
V of constants.
Let
J ![]()
![]() (H;H*) be the duality map between H and H*.
Then the annihilator
H00 = J[H1] is the m-dimensional subspace
of elements
f =
(H;H*) be the duality map between H and H*.
Then the annihilator
H00 = J[H1] is the m-dimensional subspace
of elements
f = ![]()
![]() gi where
gi where
![]()
![]()
![]() m and
g1,..., gm
m and
g1,..., gm ![]() J[V] are given by
J[V] are given by
![]() gi, u
gi, u![]() =
= ![]() ui dx, u
ui dx, u ![]() H.
H.
![]()
![]()
![]() { +
{ + ![]() } into a sum
F =
} into a sum
F = ![]() +
+ ![]() of a chemical part
of a chemical part
![]() : H
: H![]()
![]()
![]() { +
{ + ![]() }
and a nonlocal interaction part
}
and a nonlocal interaction part
![]() : H
: H ![]()
![]() as follows:
as follows:
![]() : H
: H ![]()
![]()
![]() { +
{ + ![]() } by
} by
![]() K and
M
K and
M ![]() H00
which are closed in V and J[V], respectively,
such that for all initial values u0
H00
which are closed in V and J[V], respectively,
such that for all initial values u0 ![]() K, we can define iteration
sequences
(uk)
K, we can define iteration
sequences
(uk) ![]() K and
(vk, fk)
K and
(vk, fk) ![]() C x M by
C x M by
![]()
![]()
![]() H1(
H1(![]() );H1(
);H1(![]() )*
)*![]() (including Neumann boundary conditions) given by
(including Neumann boundary conditions) given by
![]() , r > 0 and intensities
, r > 0 and intensities
![]() ,
si
,
si![]()
![]()
![]() of interaction forces
between particles of type i and
of interaction forces
between particles of type i and
![]()
![]() {0, 1,..., m}, respectively.
Clearly, both matrices
(
{0, 1,..., m}, respectively.
Clearly, both matrices
(![]() ) and
(si
) and
(si![]() ) are assumed
to be symmetric. The cases
) are assumed
to be symmetric. The cases
![]() > 0 and
> 0 and
![]() < 0
represent repulsive and attractive interaction, respectively.
The nontrivial choice of
(si
< 0
represent repulsive and attractive interaction, respectively.
The nontrivial choice of
(si![]() ) enables us
to get final states close to the corresponding initial values u0
) enables us
to get final states close to the corresponding initial values u0 ![]() K
if we define the quadratic functional
K
if we define the quadratic functional
![]() : H
: H ![]()
![]() according to (4):
according to (4):