




Next: Stochastische Teilchensysteme und Approximation der Boltzmann-Gleichung
Up: Projektbeschreibungen
Previous: Phasentrennung und kristalline Gleichgewichtsformen
Bearbeiter: A. Liemant
Kooperation: L. Brehmer (Universität Potsdam)
Beschreibung der Forschungsarbeit:
In Zusammenarbeit mit L. Brehmer von der Universität Potsdam wurden die
Untersuchungen zum Hoppingtransport von Ladungsträgern in
ungeordneten Materialien weiter betrieben. Die Ladungsträger
springen auf einem ungeordneten Gitter von räumlich und energetisch
lokalisierten Zuständen 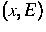 gemäß einer
Hoppingrate
gemäß einer
Hoppingrate
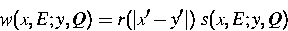
unter
Berücksichtigung des Pauliprinzips. 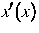 bezeichnet
die mikroskopische (makroskopische) 3-dimensionale Ortskoordinate
mit
bezeichnet
die mikroskopische (makroskopische) 3-dimensionale Ortskoordinate
mit 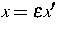 .Der Ansatz für die Hoppingrate ist recht allgemein. Es wird lediglich
gefordert, daß die Sprungweiten hinreichend klein sind (endliches
zweites Moment)
.Der Ansatz für die Hoppingrate ist recht allgemein. Es wird lediglich
gefordert, daß die Sprungweiten hinreichend klein sind (endliches
zweites Moment)
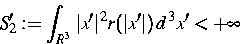
und die Hoppingrate s einer detaillierten
Gleichgewichtsbedingung
![\begin{displaymath}
\exp\Bigl[-\frac{E+e\psi({\mbox{\boldmath
$x$}})}{kT}\Bigr]...
...}\Bigr]\,s({\mbox{\boldmath
$y$}} ,Q;{\mbox{\boldmath
$x$}},E)\end{displaymath}](../../1997/html/images/img258.gif)
genügt. Eine strenge mathematische Theorie
zur Behandlung einer solchen komplexen mikroskopischen
Transportdynamik existiert gegenwärtig nicht. Wir vereinfachen,
indem wir die Dynamik mittels einer (mean field) Hoppingratengleichung
für die 1-Partikel Verteilungsfunktion beschreiben. Dies
ermöglicht es zum einen, auf einer makroskopischen Raumskala
zusätzlich
Inhomogenitäten für die Materialcharakteristiken (dies sind die
räumliche und energetische Zustandsdichte N und g(E) und die
Hoppingrate w) zu berücksichtigen. Zum anderen ist es möglich, eine
makroskopische
Drift-Diffusionsgleichung für die Ladungsdichte 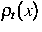 zu gewinnen,
zu gewinnen,
![\begin{align*}
\frac{\partial \varrho_t({\mbox{\boldmath$x$}})}{\partial t} =&
\...
...mbox{\boldmath$x$}}))\,\nabla
\psi({\mbox{\boldmath$x$}})
\right], \end{align*}](../../1997/html/images/img260.gif)
wobei 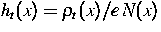 die relative Ladungsdichte
bezeichnet.
die relative Ladungsdichte
bezeichnet.
Die Gradienten der räumlichen Zustandsdichte N, des Parameters
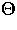 der
Energiezustandsdichte
der
Energiezustandsdichte 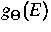 und einer Potentialfunktion
und einer Potentialfunktion
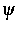 verursachen Driftströme. Der Diffusionskoeffizient D und
die Leitfähigkeiten
verursachen Driftströme. Der Diffusionskoeffizient D und
die Leitfähigkeiten 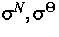 und
und 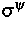 hängen explizit von den räumlich inhomogenen
Materialcharakteristiken ab, wobei D und
hängen explizit von den räumlich inhomogenen
Materialcharakteristiken ab, wobei D und 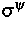 einer
verallgemeinerten Einsteinrelation genügen. Die zentrale Größe
ist die elektrische Leitfähigkeit
einer
verallgemeinerten Einsteinrelation genügen. Die zentrale Größe
ist die elektrische Leitfähigkeit
![\begin{displaymath}
\sigma^{\psi}({\mbox{\boldmath$x$}},h)= \frac{ S'_2\,e^2\,(
...
...
$x$}},h))/kT])(1+\exp[(\zeta{(\mbox{\boldmath$x$}},h)-Q)/kT])}\end{displaymath}](../../1997/html/images/img266.gif)
(e Elementarladung, k Boltzmannkonstante, T absolute Temperatur,
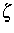 chemisches Potential).
chemisches Potential).
Projektliteratur:
- A. LIEMANT, A drift-diffusion equation for
charge transport in inhomogeneous materials, WIAS-Preprint No. 384 (1997).





Next: Stochastische Teilchensysteme und Approximation der Boltzmann-Gleichung
Up: Projektbeschreibungen
Previous: Phasentrennung und kristalline Gleichgewichtsformen
LaTeX typesetting by I. Bremer
1/18/1999
![]() gemäß einer
Hoppingrate
gemäß einer
Hoppingrate
![]()
![]()
![]()
![\begin{align*}
\frac{\partial \varrho_t({\mbox{\boldmath$x$}})}{\partial t} =&
\...
...mbox{\boldmath$x$}}))\,\nabla
\psi({\mbox{\boldmath$x$}})
\right], \end{align*}](../../1997/html/images/img260.gif)
![\begin{displaymath}
\sigma^{\psi}({\mbox{\boldmath$x$}},h)= \frac{ S'_2\,e^2\,(
...
...
$x$}},h))/kT])(1+\exp[(\zeta{(\mbox{\boldmath$x$}},h)-Q)/kT])}\end{displaymath}](../../1997/html/images/img266.gif)